Descartes's Geometric Solution of a Quadratic Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
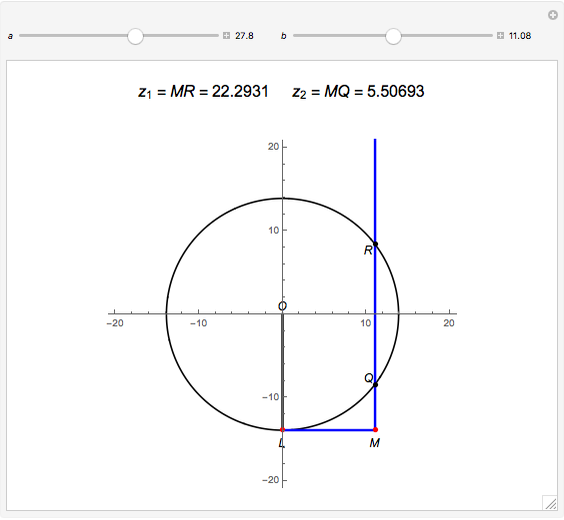
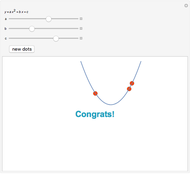
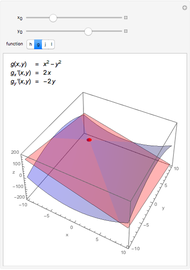
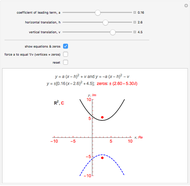
This Demonstration shows Descartes's geometric solution of the quadratic equation 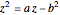 in the unknown
in the unknown  . Consider a circle of radius
. Consider a circle of radius 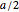 and let the points
and let the points 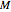 and
and  be at
be at  and
and 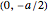 ; the circle meets the negative
; the circle meets the negative 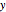 axis at
axis at  . Let the vertical line through
. Let the vertical line through 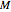 intersect the circle at
intersect the circle at 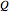 and
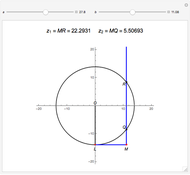
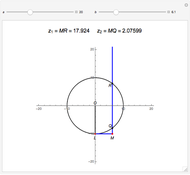
and 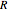 . The solutions are then given by the intersections of the circle and the line. Thus the lengths
. The solutions are then given by the intersections of the circle and the line. Thus the lengths 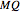 and
and 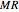 are the two roots
are the two roots 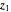 and
and  of the original quadratic equation. When
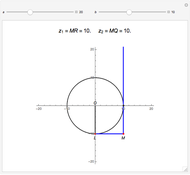
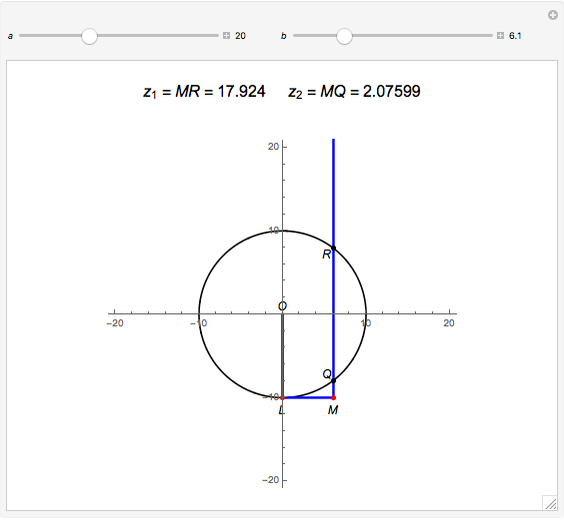
of the original quadratic equation. When  , the vertical line does not intersect the circle, meaning that the solutions to the quadratic are complex numbers. The
, the vertical line does not intersect the circle, meaning that the solutions to the quadratic are complex numbers. The  slider is therefore stopped at
slider is therefore stopped at 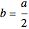 .
.
Contributed by: Bryan Chen (January 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
By Pythagoras's theorem, the  and
and 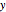 components of both points
components of both points 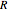 and
and 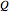 are given by
are given by  , with
, with 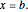 Thus
Thus 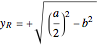 and
and  . It follows then that
. It follows then that 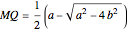 and
and 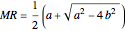 , giving the two roots of the quadratic equation.
, giving the two roots of the quadratic equation.
Reference
[1] P. J. Nahin, An Imaginary Tale: The Story of i, Princeton: Princeton University Press, 1998.
Permanent Citation