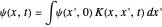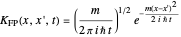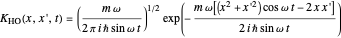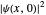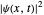Dynamics of Free Particle and Harmonic Oscillator Using Propagators

Initializing live version

The time evolution of a one-dimensional quantum system from an initial state 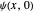can be represented, in terms of the propagator, by [1, 2]

Contributed by: S. M. Blinder (February 2020)
Open content licensed under CC BY-NC-SA

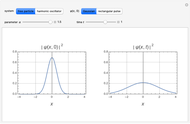
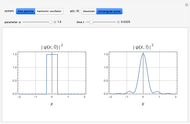
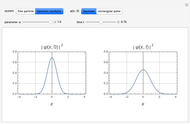
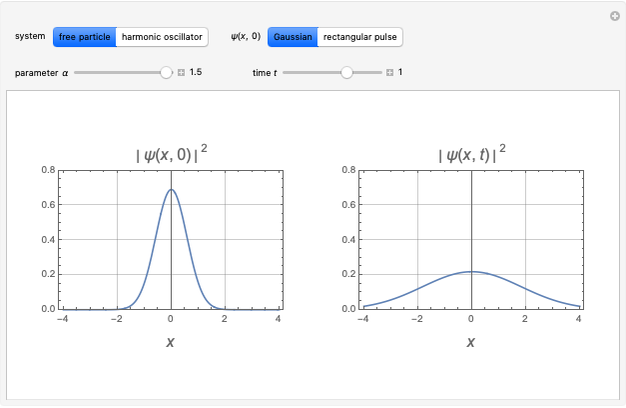
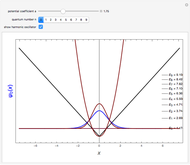
Snapshots

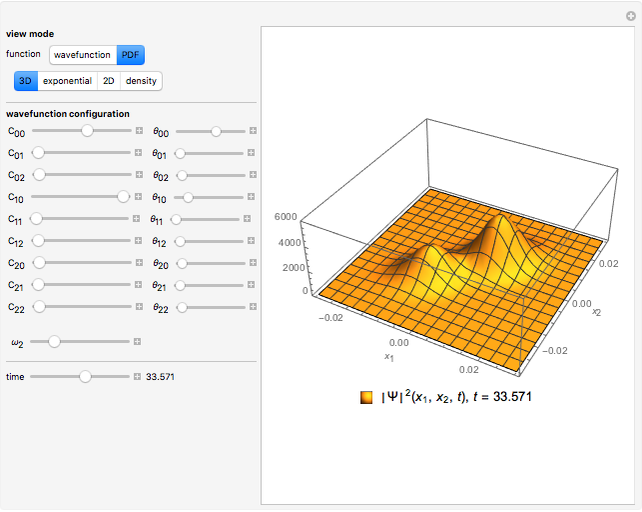
For the free particle with initial Gaussian wave packet 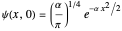, we find

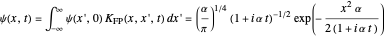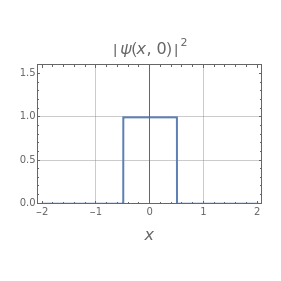
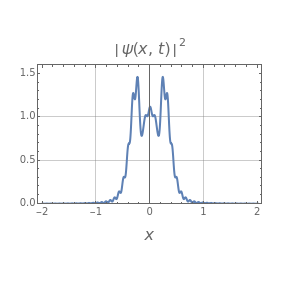
For initial rectangular pulse ,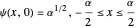

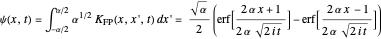For the harmonic oscillator with initial Gaussian wave packet,

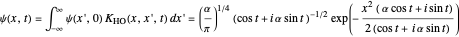(For 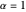, this reduces to the time-dependent ground-state eigenfunction .)

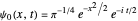For initial rectangular pulse,

References

[1] R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals, New York: McGraw-Hill, 1965.

[2] Wikipedia. "Propagator." (Feb 24, 2020) en.wikipedia.org/wiki/Propagator.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send