Harmonic-Gaussian Double-Well Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
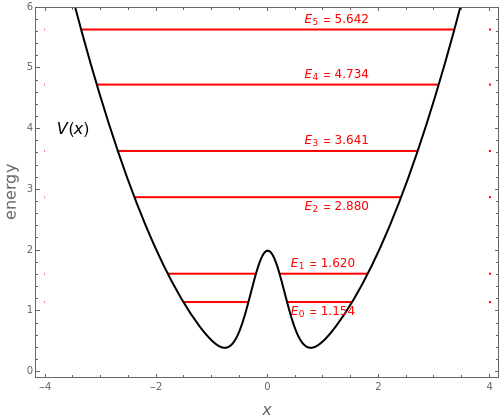
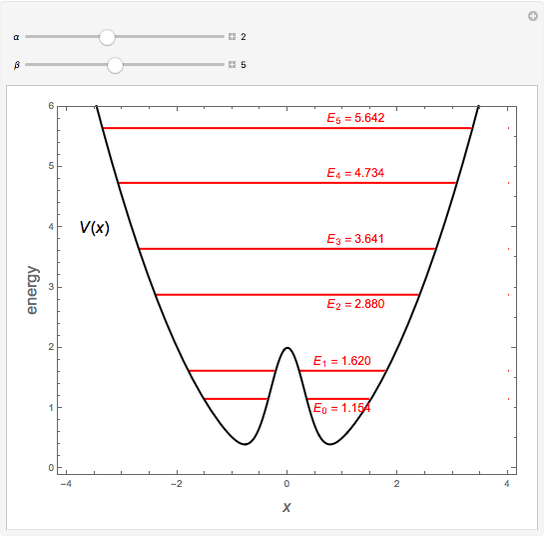
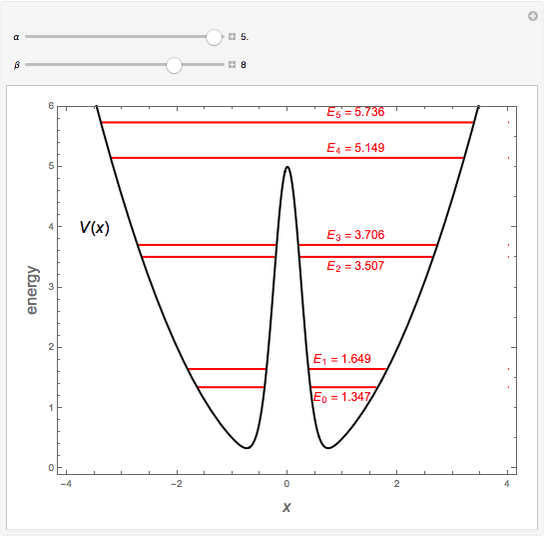
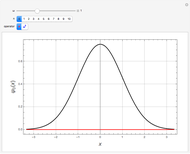
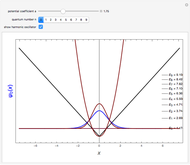
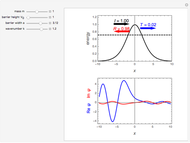
A variant of a double-well potential is a harmonic oscillator perturbed by a Gaussian, represented by the potential  . A similar function was used to model the inversion of the ammonia molecule [1]. The problem can be treated very efficiently using second-order perturbation theory based on the unperturbed harmonic oscillator. The first six energy levels are computed here.
. A similar function was used to model the inversion of the ammonia molecule [1]. The problem can be treated very efficiently using second-order perturbation theory based on the unperturbed harmonic oscillator. The first six energy levels are computed here.
Contributed by: S. M. Blinder (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
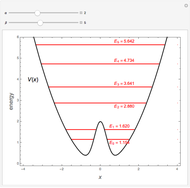
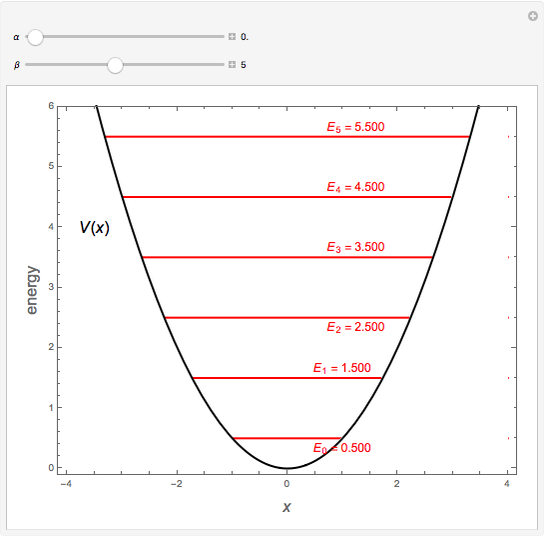
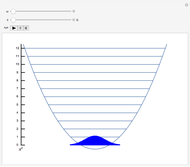
Snapshot 1: with perturbation turned off, simple harmonic oscillator with energy levels 
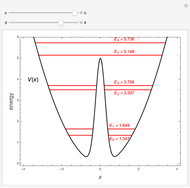
Snapshot 2: relatively small perturbation, showing convergence of levels  and
and 
Snapshot 3: larger perturbation showing approach to degeneracy of two pairs of levels
References
[1] J. D. Swalen and J. A. Ibers, "Potential Function for the Inversion of Ammonia," Journal of Chemical Physics, 36(7), 1962 pp. 1914–1918. doi:10.1063/1.1701290.
[2] K. T. Hecht, Quantum Mechanics, New York: Springer-Verlag, 2000 pp. 365–368.
[3] Wikipedia. "Perturbation Theory (Quantum Mechanics)." (Mar 11, 2013) en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics).
Permanent Citation