Three-Dimensional Isotropic Harmonic Oscillator

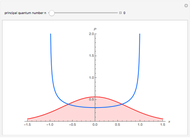
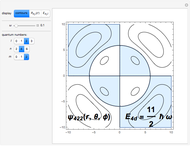
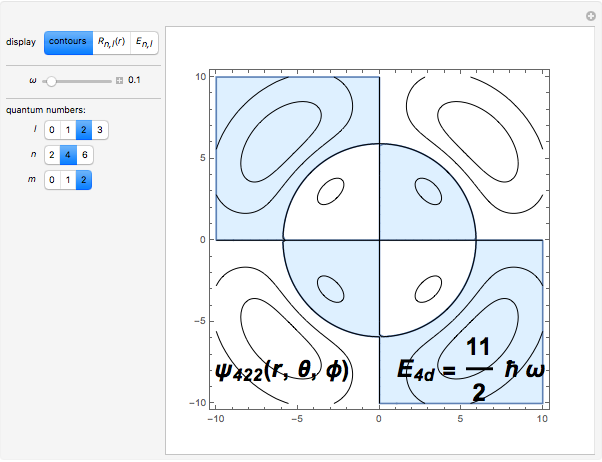
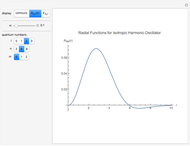
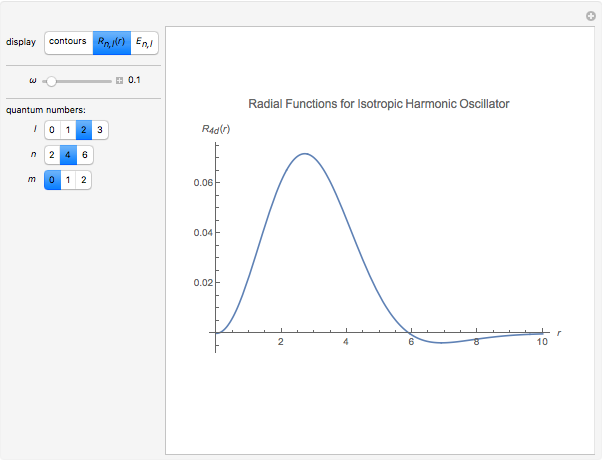
The isotropic three-dimensional harmonic oscillator is described by the Schrödinger equation , in units such that . The wavefunction is separable in Cartesian coordinates, giving a product of three one-dimensional oscillators with total energies . More interesting is the solution separable in spherical polar coordinates: , with the radial function . 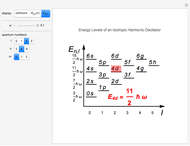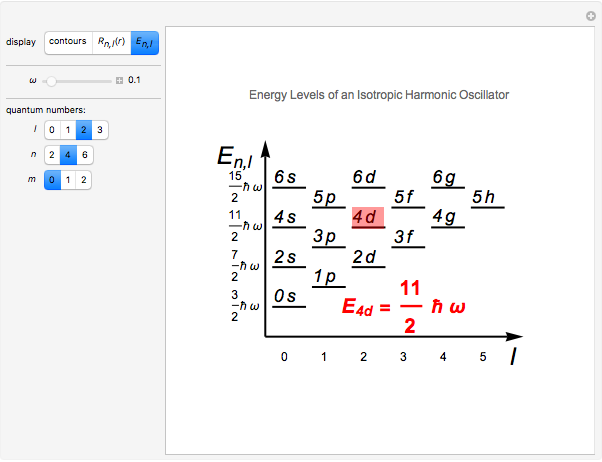Here, is an associated Laguerre polynomial, , a spherical harmonic and , a normalization constant. 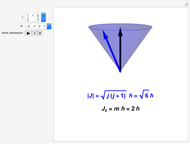The energy levels are then given by , being -fold degenerate. For a given angular momentum quantum number , the possible values of are . The conventional code is used to label angular momentum states, with representing .

This Demonstration shows contour plots in the plane for the lower-energy eigenfunctions with to . For , the eigenfunctions are complex. In all cases, the real parts of are drawn. The wavefunctions are positive in the blue regions and negative in the white regions. The radial functions are also plotted, as well as an energy-level diagram, with each dash representing the degenerate set of eigenstates for a given .

The pattern of degeneracies for a three-dimensional oscillator implies invariance under an SU(3) Lie algebra, the same as the gauge group describing the color symmetry of strong interactions.