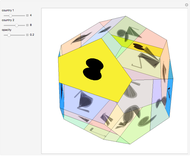
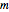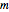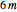A 2-pire Map

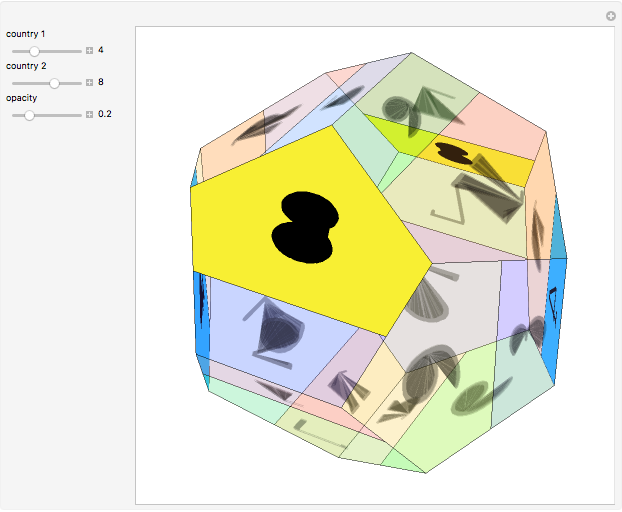
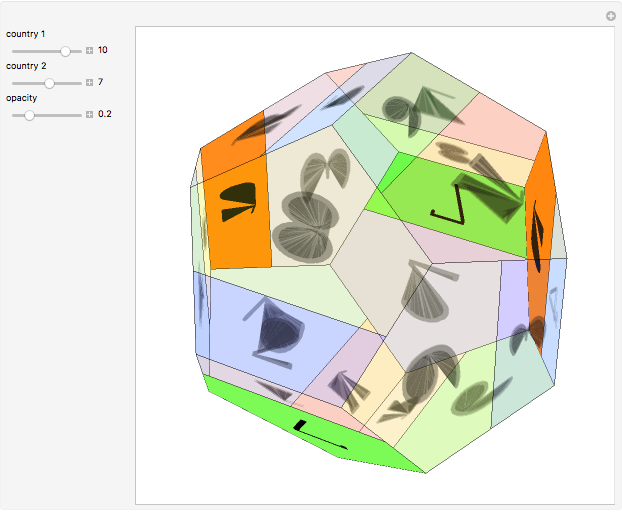
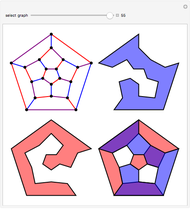
The four-color map theorem states that any map can be colored with four colors so that no two neighboring regions share a color. For a proof that four colors are necessary, consider a tetrahedron. If the faces are numbered 1 to 4, any two of these faces touch each other.

Some countries, such as the United States, consist of more than one region. On a world map, Alaska, Hawaii, and the 48 states should all have the same color. Define an -pire as a country with disconnected regions. How many colors are needed to color a world of -pires? In 1890, Percy Heawood determined that colors suffice. For 2-pires, he also showed that 12 colors were necessary.

This Demonstration shows a 12-color 2-pire map. Any two selected 2-pires share a border.