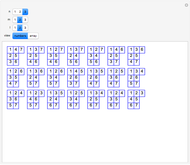
Erdös-Szekeres Tableaux

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
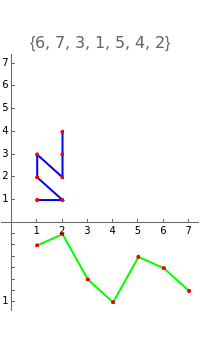
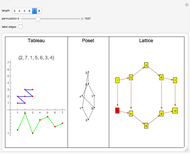
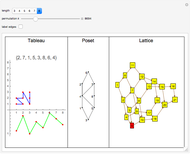
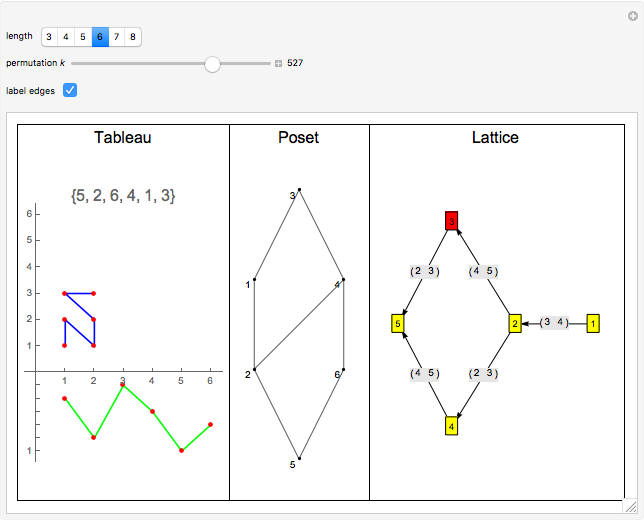
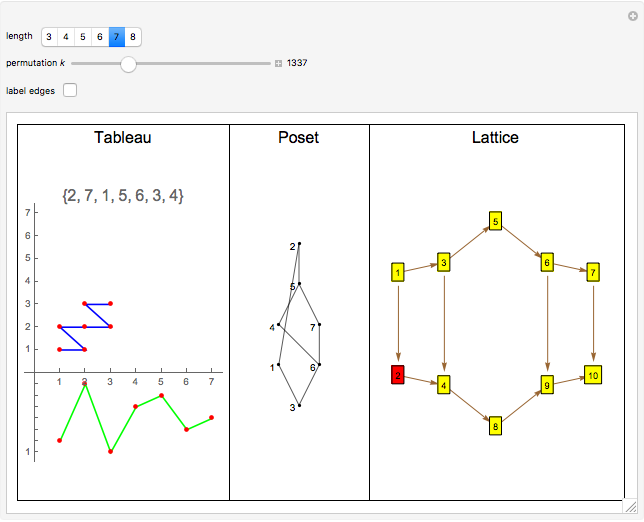
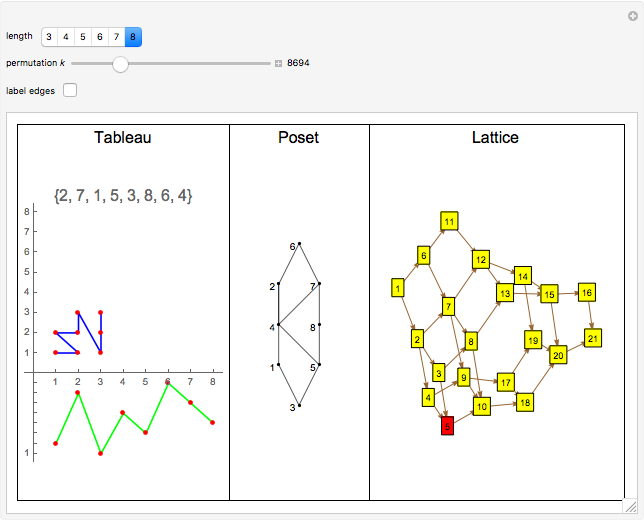
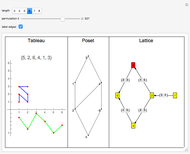
The Erdös–Szekeres tableau  of a permutation
of a permutation  is the sequence of points
is the sequence of points  where
where  (respectively
(respectively  ) is the length of the longest increasing (respectively decreasing) subsequence ending at
) is the length of the longest increasing (respectively decreasing) subsequence ending at  . Since different permutations can have the same Erdös–Szekeres tableau (EST) (e.g.
. Since different permutations can have the same Erdös–Szekeres tableau (EST) (e.g.  and
and  both have the same "N-shaped" EST), there is an equivalence relation on permutations
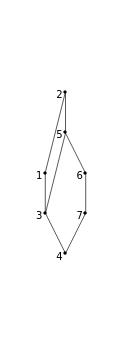
both have the same "N-shaped" EST), there is an equivalence relation on permutations  . The poset is defined by taking the intersection over all orderings induced by elements of
. The poset is defined by taking the intersection over all orderings induced by elements of  . Informally, the poset records those relations that can be recovered from the EST. The lattice is defined on
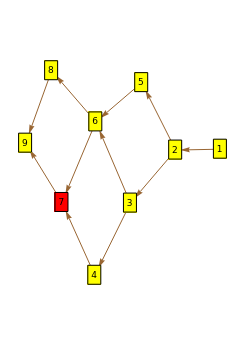
. Informally, the poset records those relations that can be recovered from the EST. The lattice is defined on  , where
, where  is in the covering relation if
is in the covering relation if  and
and  differ by an adjacent transposition (which can be viewed as an edge label) and
differ by an adjacent transposition (which can be viewed as an edge label) and  precedes
precedes  lexicographically.
lexicographically.
Contributed by: Benjamin Shemmer (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration illustrates concepts developed in [1]. The green curve in the first pane visualizes a permuatation  by plotting the points
by plotting the points  for
for  .
.
Reference
[1] S. V. Ault and B. Shemmer, "Erdös–Szekeres Tableaux," Order, 13, 2013. doi: 10.1007/s11083-013-9308-2.
Permanent Citation