Van der Waerden's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Van der Waerden's theorem states that for positive integers 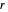 and
and  there exists an integer
there exists an integer 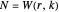 such that any
such that any  -coloring of the integers
-coloring of the integers  contains a monochromatic arithmetic progression (MAP) of length
contains a monochromatic arithmetic progression (MAP) of length  . The current best-known bounds on
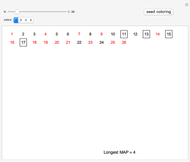
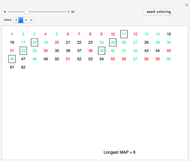
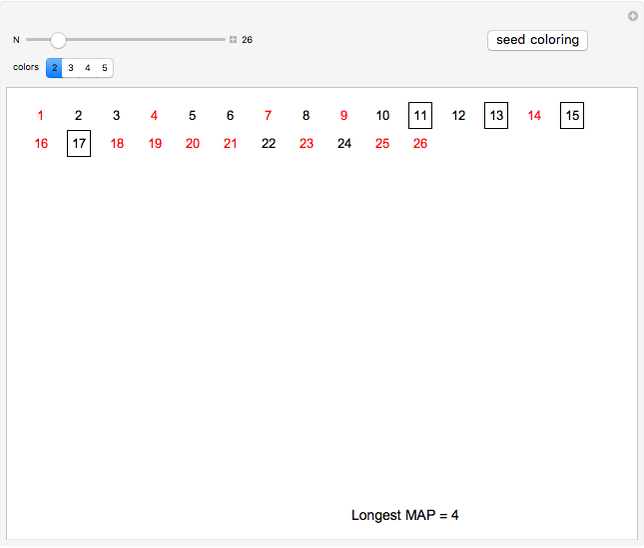
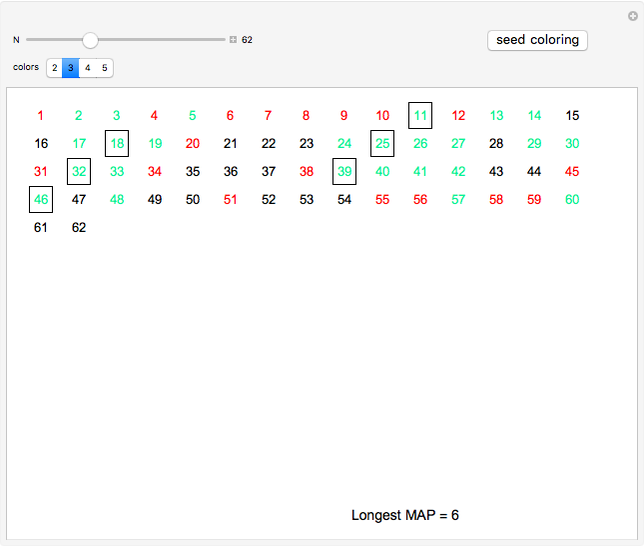
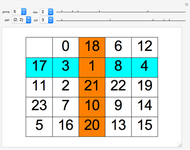
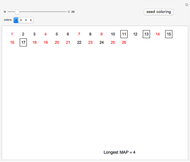
. The current best-known bounds on 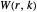 are large power towers; very few specific values are known. After seeding a random coloring, you can click a number to cycle through other colors. See if you can find a 3-coloring of 1 through 26 with no MAP of length 3, thus showing
are large power towers; very few specific values are known. After seeding a random coloring, you can click a number to cycle through other colors. See if you can find a 3-coloring of 1 through 26 with no MAP of length 3, thus showing 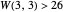 . What about extremal colorings for
. What about extremal colorings for 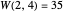 ,
, 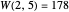 , and
, and 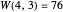 ?
?
Contributed by: Benjamin Shemmer (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation