Estimating a Distribution Function Subject to a Stochastic Order Restriction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
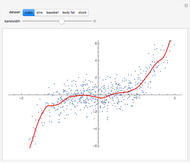
This Demonstration shows the nonparametric estimation of a standard normal variable cumulative distribution function (CDF) 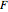 , under a stochastic order restriction. A pseudorandom data generation process produces a standard normal variable
, under a stochastic order restriction. A pseudorandom data generation process produces a standard normal variable 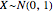 with distribution function
with distribution function 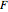 and data size
and data size  , and a uniform variable
, and a uniform variable 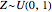 with data size
with data size 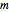 . Mathematica's built-in inverse normal distribution function utilizes
. Mathematica's built-in inverse normal distribution function utilizes  to generate another normal variable
to generate another normal variable 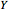 with distribution function
with distribution function 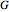 and data size
and data size 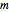 , under the stochastic restriction
, under the stochastic restriction 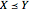 (
( ). This restriction may be imposed by three different shift patterns (see Details).
). This restriction may be imposed by three different shift patterns (see Details).
Contributed by: Michail Bozoudis and Vasileios Papachatzis (July 2015)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration (based on [1]) shows the performance of four nonparametric estimators on a distribution function 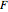 , subject to a stochastic order restriction. The estimators are:
, subject to a stochastic order restriction. The estimators are:
• the usual (unrestricted) empirical distribution function (EDF) estimator, 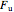
• the nonparametric maximum likelihood estimator (np-MLE), 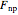 ([2])
([2])
• the pointwise maximum likelihood estimator (p-MLE), 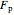 ([3])
([3])
• and the switch maximum likelihood estimator (s-MLE), 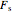 ([4])
([4])
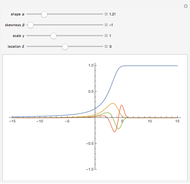
While 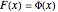 , the order restriction
, the order restriction  may be imposed according to three shift (
may be imposed according to three shift (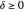 ) alternatives:
) alternatives:
• 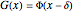 , denoted as the "difference" shift pattern
, denoted as the "difference" shift pattern
• 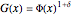 , denoted as the "power" shift pattern
, denoted as the "power" shift pattern
•  for
for 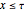 and
and 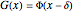 for
for  , denoted as the "tail" shift pattern
, denoted as the "tail" shift pattern
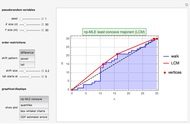
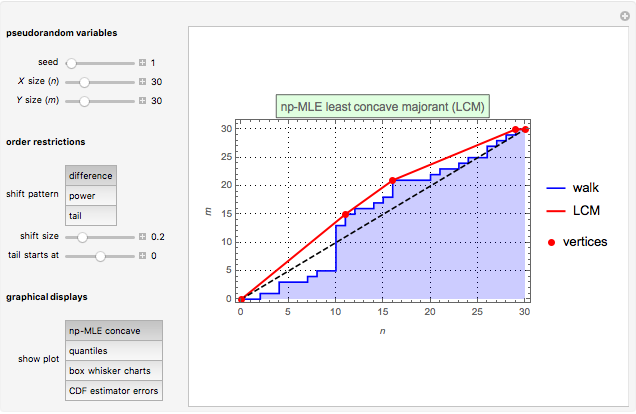
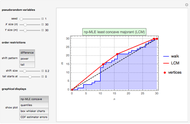
The first graphic displays the construction of the np-MLE least concave majorant (LCM) according to the 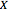 ,
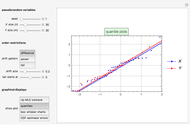
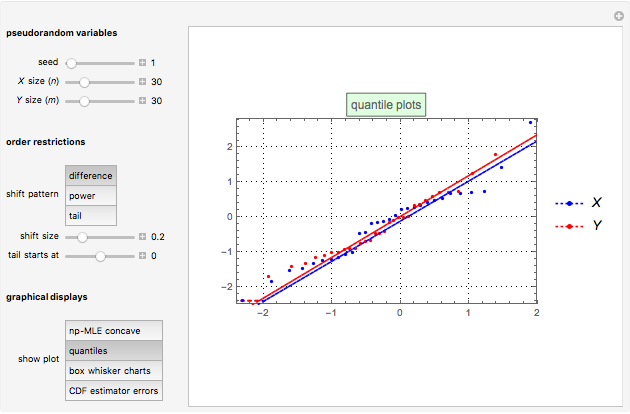
, 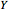 ordered random walk. The second graphic displays the quantile plots for
ordered random walk. The second graphic displays the quantile plots for 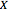 and
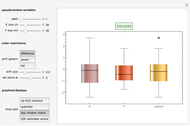
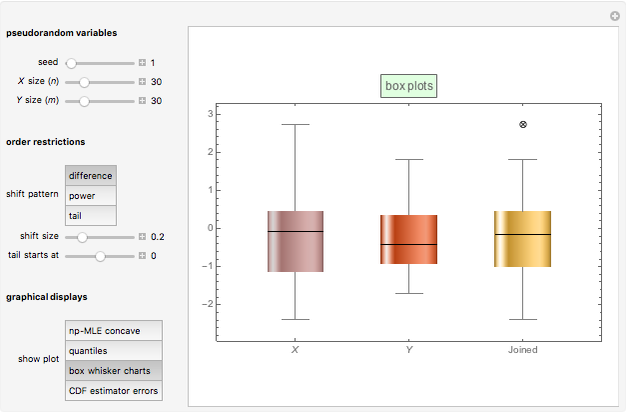
and 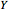 . The third graphic displays the box plots for
. The third graphic displays the box plots for 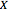 ,
, 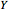 , and
, and  . Finally, the fourth graphic displays the estimator errors against the theoretical standard normal quantiles.
. Finally, the fourth graphic displays the estimator errors against the theoretical standard normal quantiles.
References
[1] O. Davidov and G. Iliopoulos, "Estimating a Distribution Function Subject to a Stochastic Order Restriction: A Comparative Study," Journal of Nonparametric Statistics, 24(4), 2012 pp. 923–933.
[2] H. D. Brunk, W. E. Franck, D. L. Hanson, and R. V. Hogg, "Maximum Likelihood Estimation of the Distributions of Two Stochastically Ordered Random Variables," Journal of the American Statistical Association, 61(316), 1966 pp. 1067–1080.
[3] R. V. Hogg, "On Models and Hypotheses with Restricted Alternatives," Journal of the American Statistical Association, 60(312), 1965 pp. 1153–1162.
[4] S. Lo, "Estimation of Distribution Functions under Order Restrictions," Statistics & Risk Modeling, 5(3–4), 1987 pp. 251–262.
Permanent Citation