Closed-Form Full Life Cycle Distribution


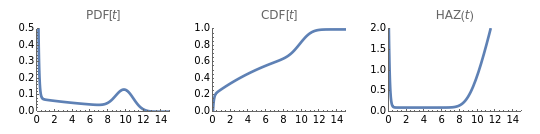
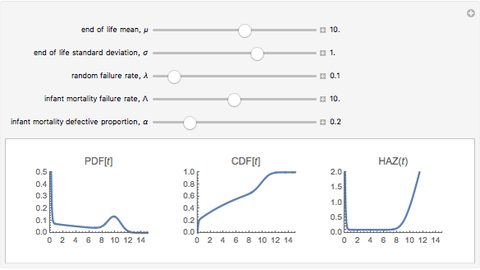
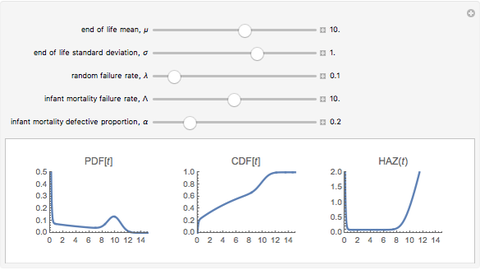
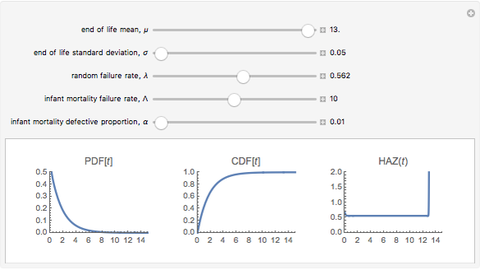
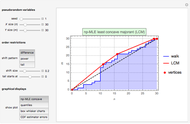
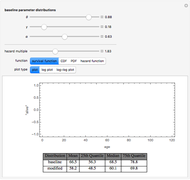
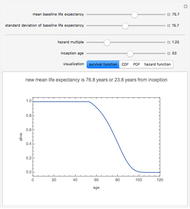
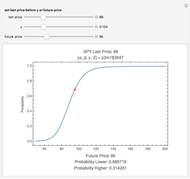
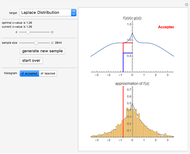
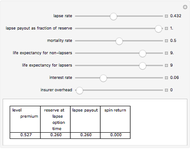
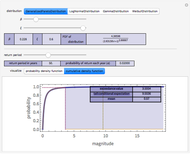
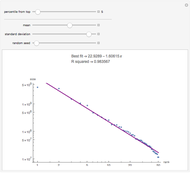
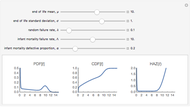
	This Demonstration features an approximation of the closed-form full life cycle distribution. It updates the probability density function, cumulative density function, and hazard function for the distribution as you change the five input parameters. This distribution models the three basic types of failure—infant mortality, random, and end-of-life. It is a rigorous improvement over the empirically observed and modeled "bathtub curve". Like the related Weibull distribution, it is closed-form and continuous; unlike the Weibull, it can simultaneously model infant mortality and wear-out. This distribution closely approximates the closed-form full life cycle distribution when the wear-out mean is significantly larger than the wear-out standard deviation.


	Contributed by: Kelly S. Lowder

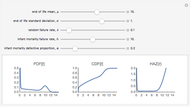
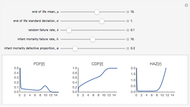
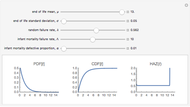
The first snapshot depicts the effects of infant mortality, random failure, and wear-out on the distribution. The second snapshot demonstrates that when the random failure rate is relatively high, the distribution asymptotically approaches an exponential. The third snapshot shows that when infant mortality and random failures are low, wear-out dominates, and the distribution approaches a Gaussian.