Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

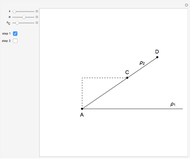
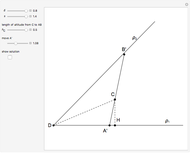
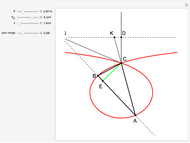
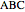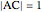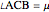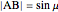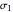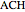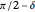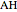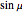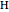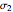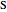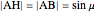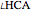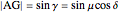Find the Angle Whose Sine is the Product of the Sine and Cosine of Two Other Angles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

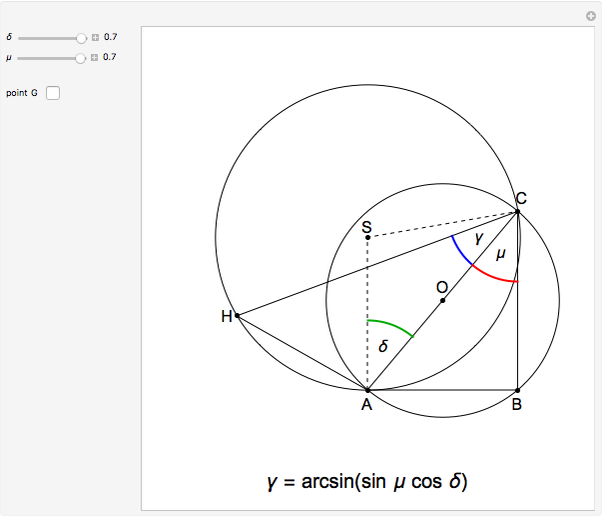
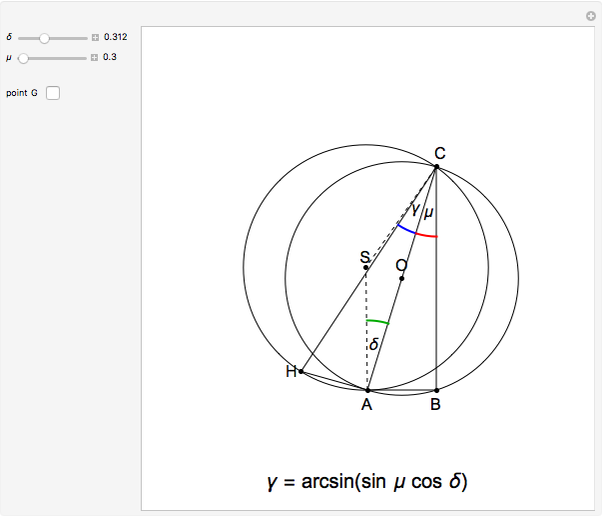
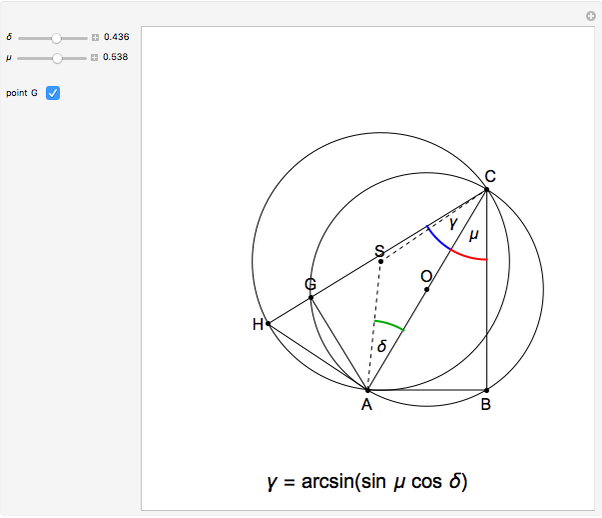
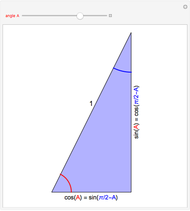
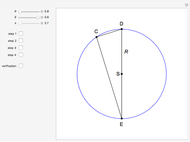
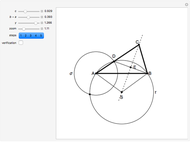
This Demonstration shows a geometric solution of the trigonometric equation 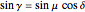, where is unknown.

[more]

Draw a right-angle triangle with the hypotenuse and . Then . Let be the circumcircle of .

Transform the equation to and interpret it as the law of sines for a triangle with of length 1 opposite the angle and side of length opposite the unknown angle .

To find the point , draw a circle with inscribed angle over the chord . Let be the center of . Construct the point on so that . By the law of sines, the angle at is a solution for .

If is the intersection of and , then . You can choose to show the point .

[less]

Contributed by: Izidor Hafner (July 2017)
Open content licensed under CC BY-NC-SA

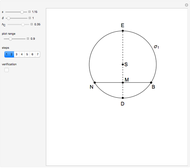
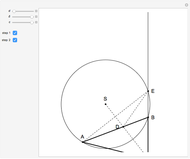
Snapshots

Details

The idea for this Demonstration comes from [1].

Reference

[1] J. Plemelj, Iz mojega življenja in dela (From My Life and Work), Obzornik mat. fiz., 39, 1992 pp. 188–192.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send