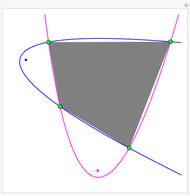
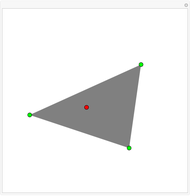
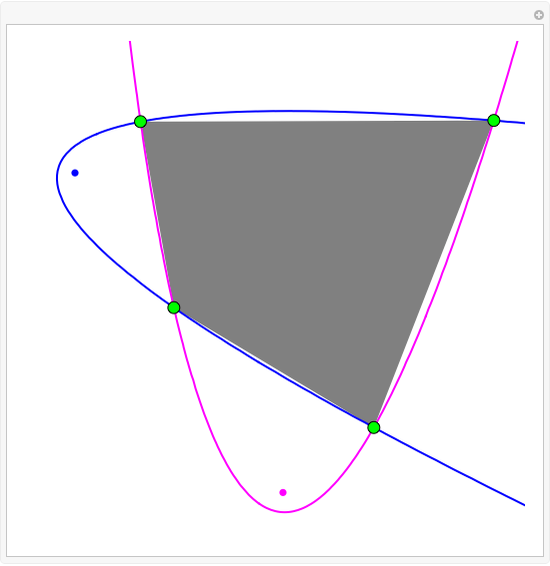
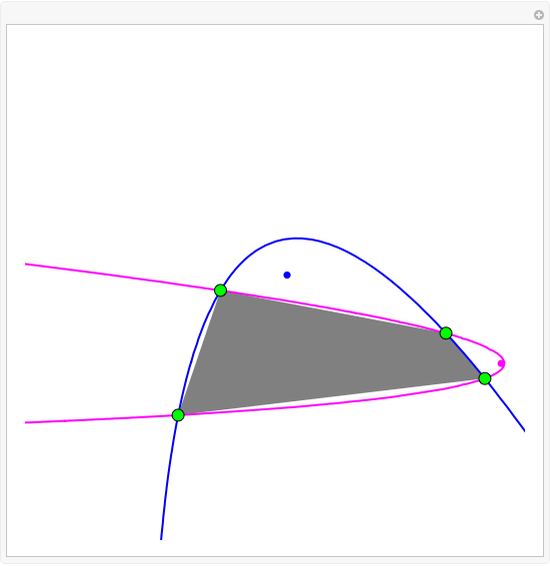
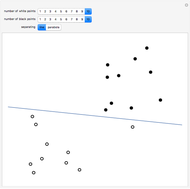
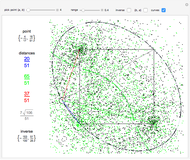
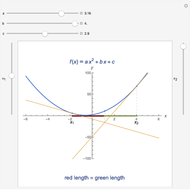
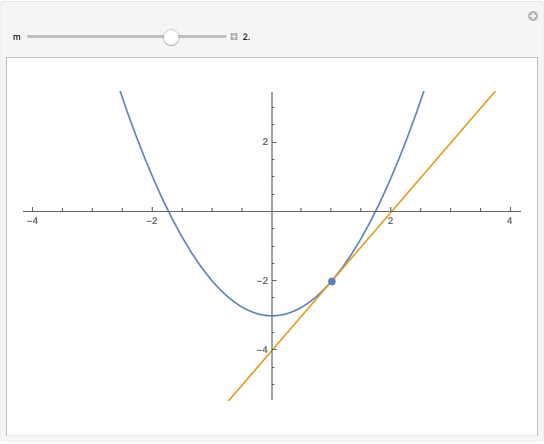
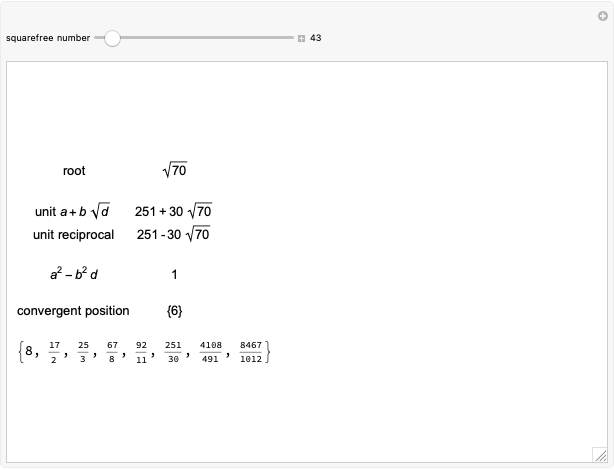
Isaac Newton explicitly constructed four-point parabolas in Arithmetica Universalis (1707). In this Demonstration, you can drag four points that define two parabolas most of the time. By Sylvester's four-point theorem, the points form a concave set with odds 25/36. The corners of a rectangle also cannot be on a parabola. The precise odds that four random points can define a parabola appears to be an unsolved problem.