Mamikon's Method for the Area under a Parabola

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
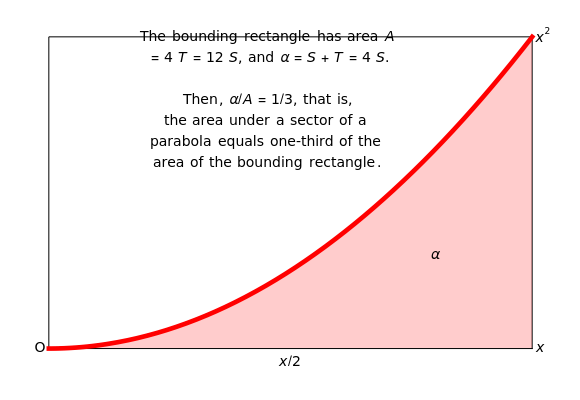
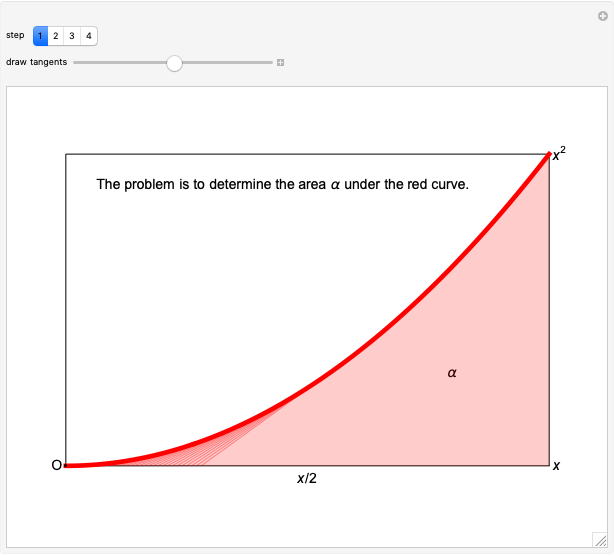
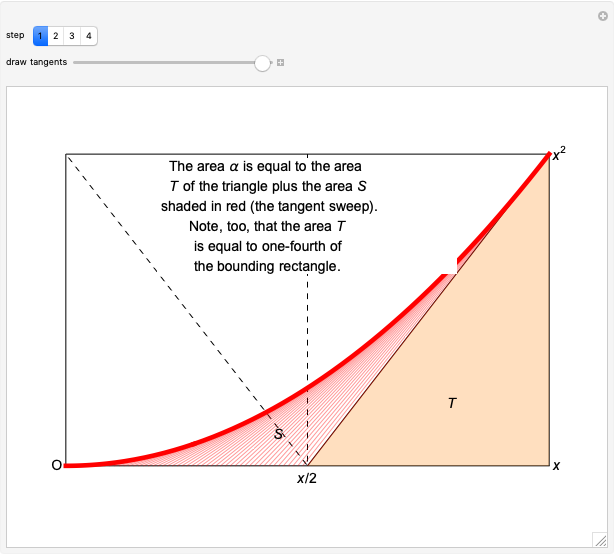
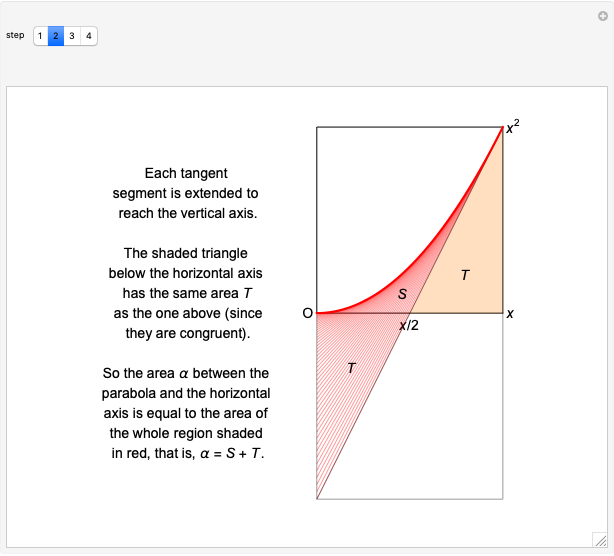
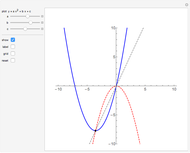
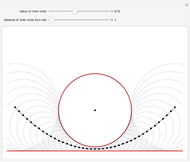
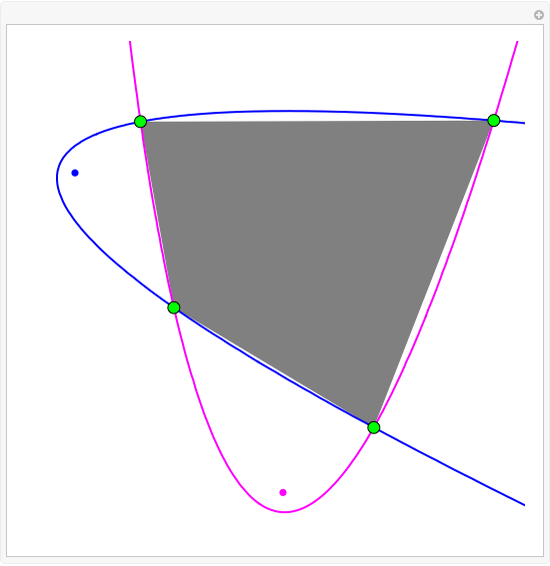
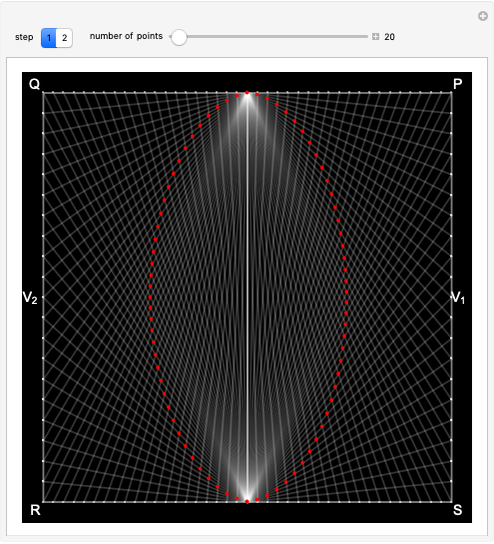
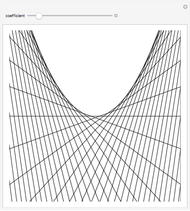
The area under a parabola is determined without recourse to calculus, using only geometric concepts.
Contributed by: Tomas Garza (February 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
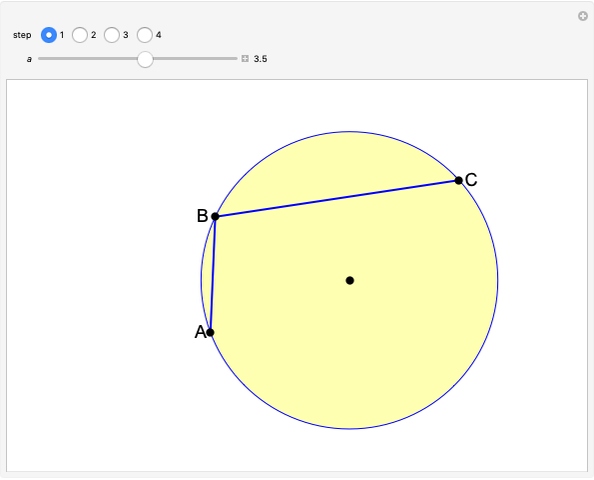
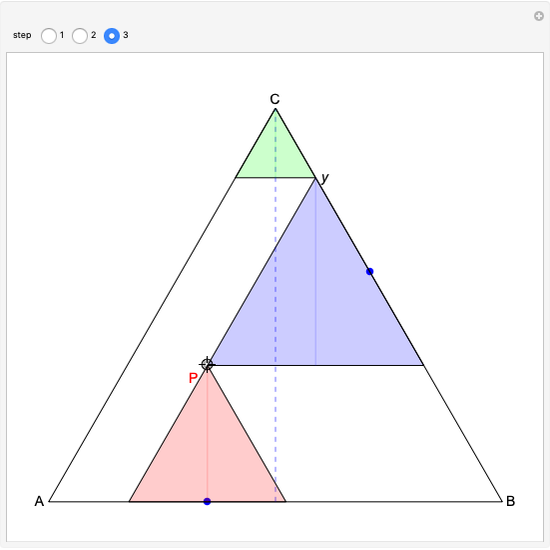
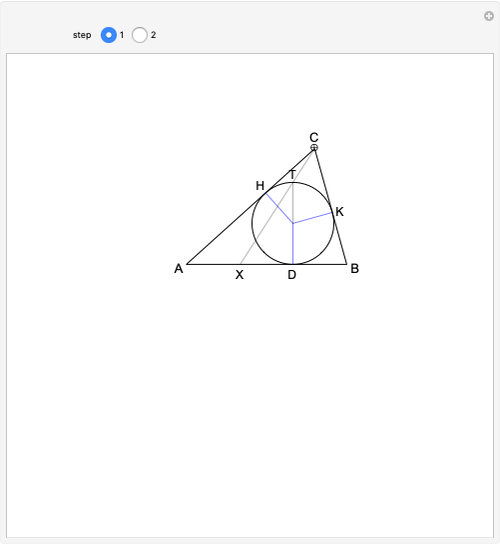
In 1959, Mamikon Matsakanian, generally known as Mamikon, devised an original method for solving problems in geometry. This is described in full in [1]. This Demonstration presents an example in which the area under a parabola is obtained using only elementary concepts of geometry.
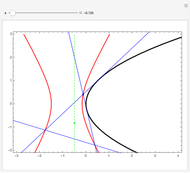
A result used in the Demonstration is the scaling property, which says that if each tangent segment of a tangent sweep is scaled (expanded or contracted) by the same positive factor  , then the area of the tangent sweep is multiplied by
, then the area of the tangent sweep is multiplied by  [1, p. 19].
[1, p. 19].
Reference
[1] T. M. Apostol and M. Matsakanian, New Horizons in Geometry, Washington, DC: The Mathematical Association of America, 2012.
Permanent Citation