Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

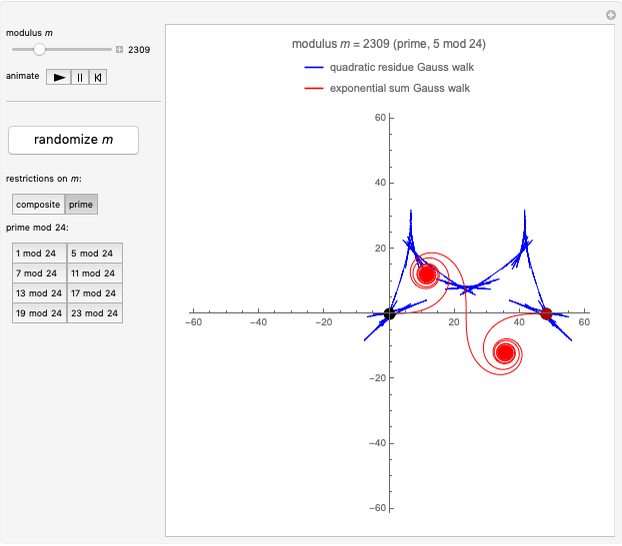
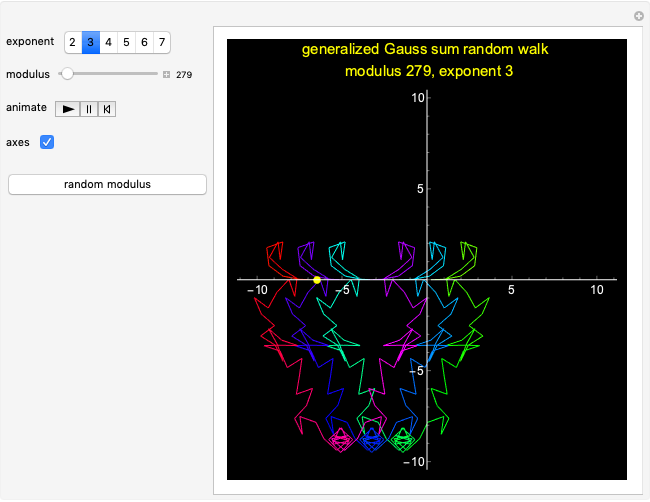
Pseudorandom Walks with Generalized Gauss Sums

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

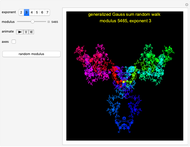
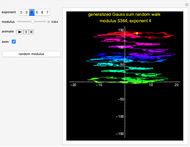
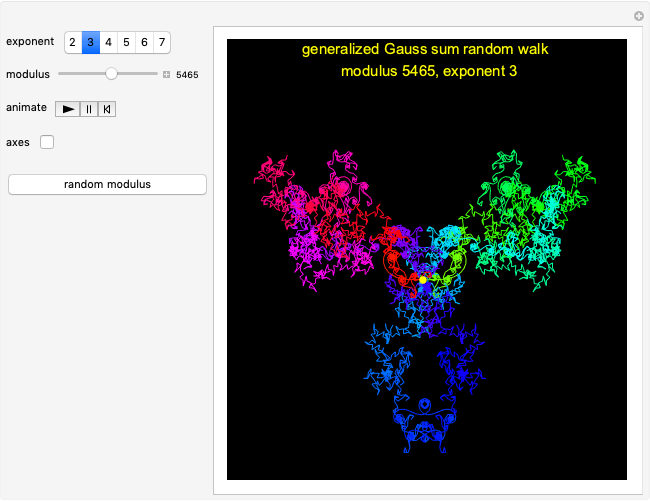
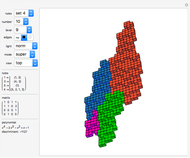
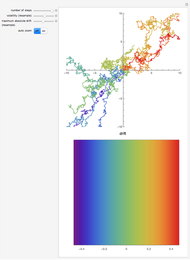
This Demonstration shows pseudorandom walks constructed from generalized Gauss sums, defined by , where the modulus and the exponent are integers of at least 2. (The case reduces to the classical quadratic Gauss sum.)

[more]

The random walks start at the origin, then the end point, as indicated by the yellow dot, takes steps given by the terms of the sum. The walks exhibit complicated behavior with curlicue patterns and sometimes unexpected symmetries.

[less]

Contributed by: Ka Fung Tjin (June 2020)
(Based on an undergraduate research project at the Illinois Geometry Lab by Ka Fung Tjin, Erqian Wang and Yifan Zhang and directed by A. J. Hildebrand.)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This Demonstration is inspired by visualizations from [1].

[1] R. R. Moore and A. J. van der Poorten, "On the Thermodynamics of Curves and Other Curlicues," Miniconference on Geometry and Physics (M. N. Barber and M. K. Murray, eds.), Canberra, Australia: The Australian National University, 1989 pp. 82–109. maths.anu.edu.au/files/CMAProcVol22-MoorePoorten.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send