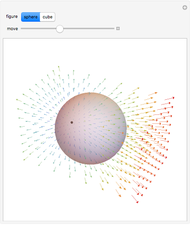
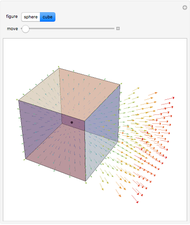
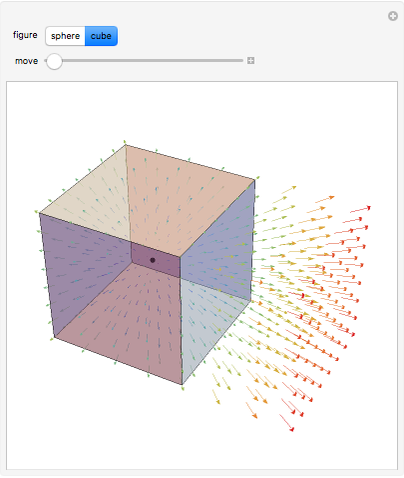
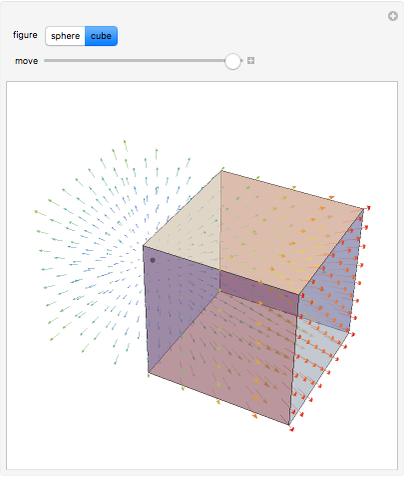
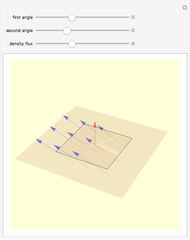
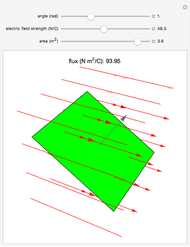
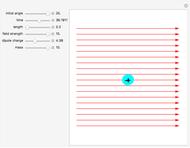
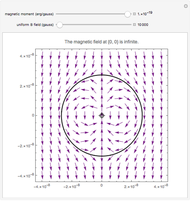
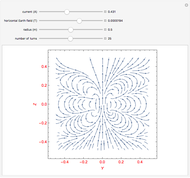
The net electric flux through any closed surface is proportional to the charge enclosed by the surface (in this case a sphere or a cube). Notice that when the charge is inside the surface, all vectors representing the electric flux point outward, but when the surface is moved and no longer encloses the charge, the flux entering one side exits the opposite side and the net flux equals zero.