Spontaneous Emission in a Free-Electron Laser

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
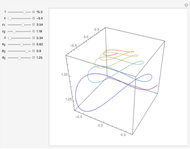
This Demonstration shows an electron bunch entering an undulator magnet (represented by a sinusoid with period 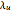 ). The electrons experience a Lorentz force (assuming the magnetic field is directed vertically) and execute transverse oscillations in the horizontal plane. The emission process is characterized by antenna lobe emission, which is more intense when the acceleration is greater. The process can be described either in the laboratory or in the electron rest frame. In the latter case, the electrons "see" the undulator field as an incoming electromagnetic wave with a wavelength that is linked to the undulator Lorentz contracted period.
). The electrons experience a Lorentz force (assuming the magnetic field is directed vertically) and execute transverse oscillations in the horizontal plane. The emission process is characterized by antenna lobe emission, which is more intense when the acceleration is greater. The process can be described either in the laboratory or in the electron rest frame. In the latter case, the electrons "see" the undulator field as an incoming electromagnetic wave with a wavelength that is linked to the undulator Lorentz contracted period.
Contributed by: Marcello Artioli, Giuseppe Dattoli,andSimonetta Pagnutti (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In a free-electron laser (FEL), light amplification is produced by high-energy electrons propagating through magnetic structures [1] (rather than by population inversion, as in an atomic or molecular medium).
The essential elements of a FEL are, therefore, a beam of relativistic electrons and an undulator, a magnetic device producing an oscillating magnetic field along the  axis:
axis:
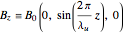 , (1)
, (1)
where  and
and 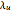 are the field amplitude and the undulator period, respectively. The undulator is characterized by
are the field amplitude and the undulator period, respectively. The undulator is characterized by 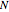 periods and therefore has a total length
periods and therefore has a total length  .
.
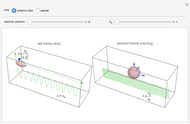
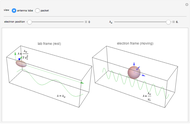
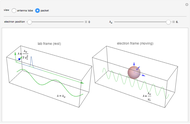
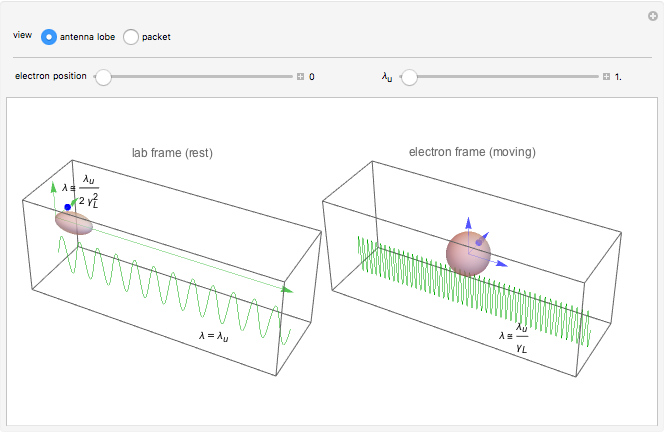
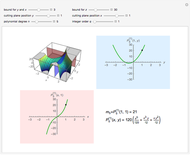
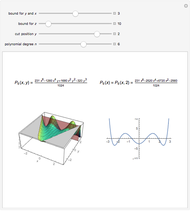
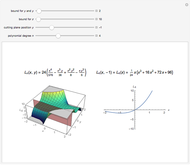
The electrons originally moving longitudinally along the  axis (first figure) experience the Lorentz force and acquire a transverse component of motion. This acceleration causes the electrons to emit flashes of synchrotron radiation, which are more intense for higher accelerations (second figure).
axis (first figure) experience the Lorentz force and acquire a transverse component of motion. This acceleration causes the electrons to emit flashes of synchrotron radiation, which are more intense for higher accelerations (second figure).
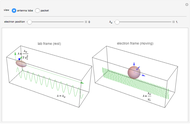
The peculiar features of the radiation emitted by the electrons inside the undulator can be understood as follows:
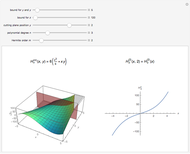
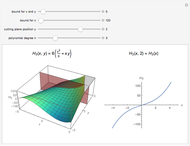
a) The electrons in their “rest” frame perceive the undulator field as a transverse wave, which determines the charge oscillations shown in the first figure and the associated dipole radiation emission (indicated by an antenna lobe).
b) The wavelength of the emitted radiation is the same as the incident radiation, which is associated with the Lorentz-contracted length of the undulator period, namely
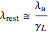 , (2)
, (2)
where 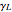 is the longitudinal Lorentz factor.
is the longitudinal Lorentz factor.
c) Returning back to the lab frame (second figure) the emitted radiation undergoes a further contraction of wavelength and emission angle in the forward direction, shown by the elongated shape of the antenna dipole emission.
To summarize, we find for the emitted wavelength in the lab frame
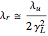 , (3)
, (3)
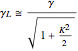 , (4)
, (4)
where  is the electron Lorentz factor and
is the electron Lorentz factor and  is the so-called “undulator parameter”; the terms under the square root account for the transverse motion, induced by the undulator field with
is the so-called “undulator parameter”; the terms under the square root account for the transverse motion, induced by the undulator field with 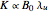 [2].
[2].
The emitted radiation has, accordingly, very peculiar characteristics, namely:
1) The radiation emitted by the electrons moves a little faster than the electrons themselves (first figure), therefore after traversing the entire undulator length, the photons will be ahead of the electron bunch by a distance
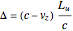 , (5)
, (5)
which is called the “slippage distance,” with  the electron longitudinal velocity. From the temporal point of view, the radiation profile is that of a wave train of duration
the electron longitudinal velocity. From the temporal point of view, the radiation profile is that of a wave train of duration  .
.
2) The slippage distance, given by equation (5), can be calculated from special relativity, using the relation
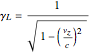 , (6)
, (6)
so that
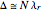 . (7)
. (7)
The pulse duration and its spectral width  are linked by the Parseval identity:
are linked by the Parseval identity:
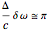 . (8)
. (8)
The spectral profile is therefore a narrow peak around the frequency
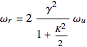 , (9)
, (9)
with
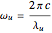 . (10)
. (10)
Since the spectral width of the peak is inversely proportional to  , we get for the relative bandwidth
, we get for the relative bandwidth
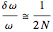 . (11)
. (11)
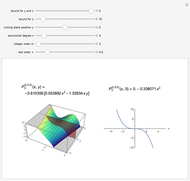
The spectral shape of the radiation emitted by the electron in an undulator is, accordingly, that of the finite duration process characterized by a profile
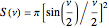 with
with 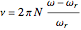 , (12)
, (12)
where  is a dimensionless quantity, called the “detuning parameter.”
is a dimensionless quantity, called the “detuning parameter.”
In conclusion, the electrons inside an undulator magnet emit radiation. According to equations (9) and (10), the emission frequency can be tuned by varying the electron energy and the undulator period (and the on-axis magnetic field intensity as well). The intensity of the emitted radiation depends on classical parameters, such as the intensity of the magnetic field, the electron energy, the number of periods, and the current inherent in the electron beam.
References
[1] W. B. Colson, Classical Free Electron Laser Theory, book chapter in Laser Handbook Vol. 6, ed. by W. B. Colson, C. Pellegrini, and A. Renieri, Amsterdam: North-Holland, 1990.
[2] G. Dattoli, A. Renieri, and A. Torre, Lectures on the Free Electron Laser Theory and Related Topics, Singapore: World Scientific, 1993.
Permanent Citation