Hilbert and Moore Fractal Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
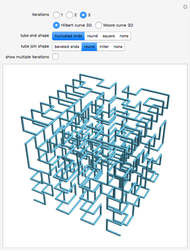
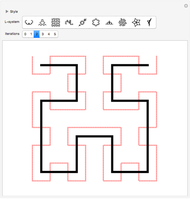
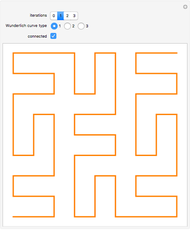
The Hilbert curve and the Moore curve are two famous plane-filling curves. They have similar recursive constructions, constructed here using L-systems. Such curves map points in multi-dimensional space to points on a one-dimensional line, and thus have properties that make them useful for certain types of data manipulation (such as image processing).
Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
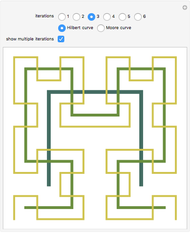
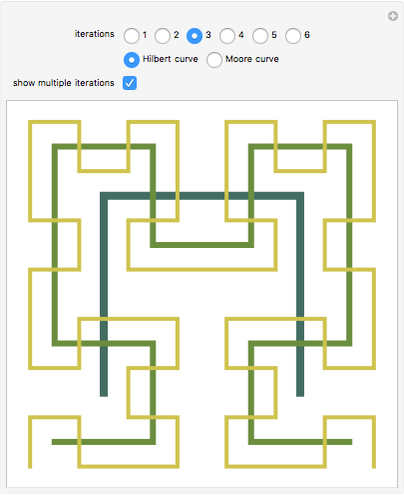
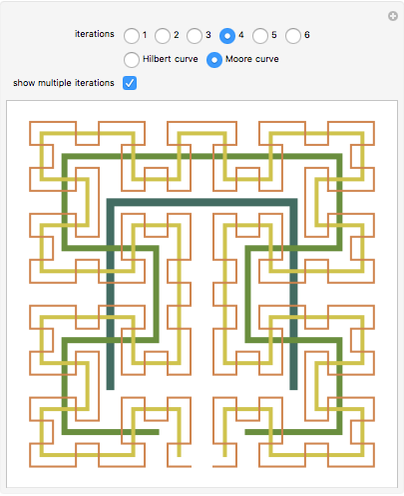
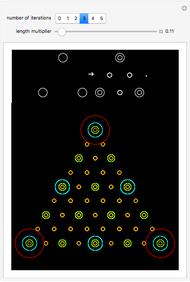
Snapshot 1: Viewing multiple iterations at once can assist in making the recursive construction of the curves clearer.
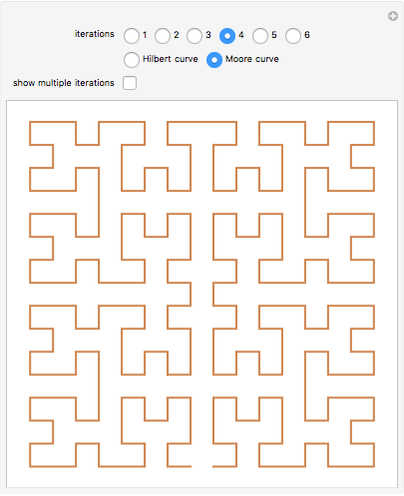
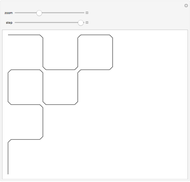
Snapshot 2: One way in which the Hilbert curve and Moore curve differ is in the relative positions of the start and end points of the curve. While the Hilbert curve begins and ends in adjacent corners of the bounding square, the Moore curve begins and ends in adjacent points in the resulting grid.
Snapshot 3: In this Demonstration, the Hilbert curve and the Moore curve begin with the same initial shape; it can be illuminating to switch between the Hilbert and Moore figures for a given iteration level.
The Lebesgue curve has similar properties; while the Lebesgue mapping is easier to compute, the Hilbert curve is often desirable in that no two consecutive points are very far apart.
Permanent Citation
"Hilbert and Moore Fractal Curves"
http://demonstrations.wolfram.com/HilbertAndMooreFractalCurves/
Wolfram Demonstrations Project
Published: March 7 2011