Lebesgue 3D Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
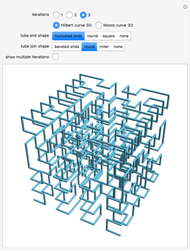
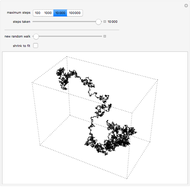
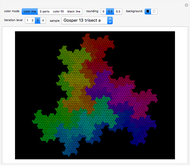
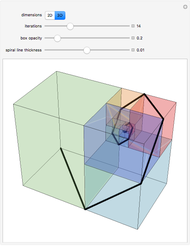
The Lebesgue curve in three dimensions is a space-filling curve, similar to the Hilbert curve in three dimensions. The curve maps points in multi-dimensional space to points on a one-dimensional line, and has properties that make it useful in computer science for algorithms that operate on one-dimensional data.
Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
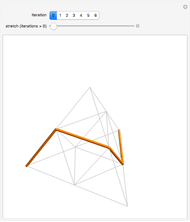
Snapshot 1: Construction of the 3D Lebesgue curve begins with the eight corners of a cube connected in a specific order.
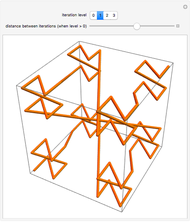
Snapshot 2: Each subsequent iteration is created by placing a copy of the initial shape at each corner of a cube, and then connecting the last point one of one copy with the first point of the next copy, where the order in which the copies are connected is the same order in which the points in the level-zero construction are connected. (Adjusting the distance between iterations reveals the recursive nature of the construction.)
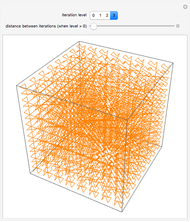
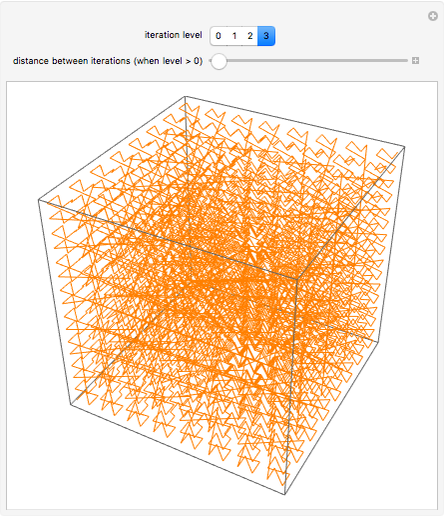
Snapshot 3: With greater iteration levels, it is apparent that the curve visits every point in the cube. (Rendering the curve with lines is faster than rendering with cylinders and spheres, which is useful for visualizing greater iteration levels on slower systems.)
Permanent Citation
"Lebesgue 3D Curves"
http://demonstrations.wolfram.com/Lebesgue3DCurves/
Wolfram Demonstrations Project
Published: March 7 2011