Folding a Strip of Unlabeled Stamps

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
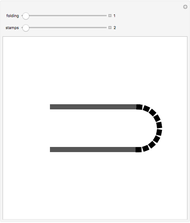
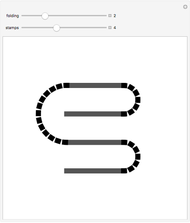
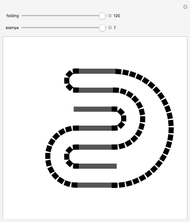
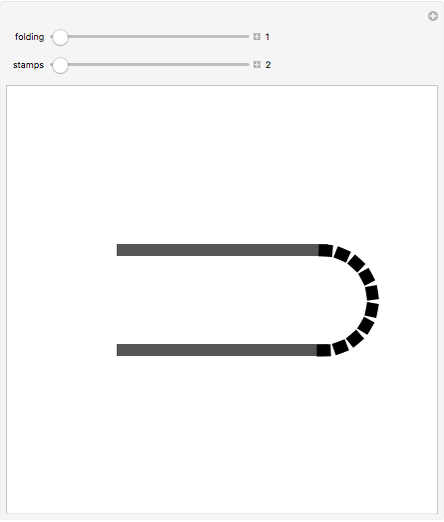
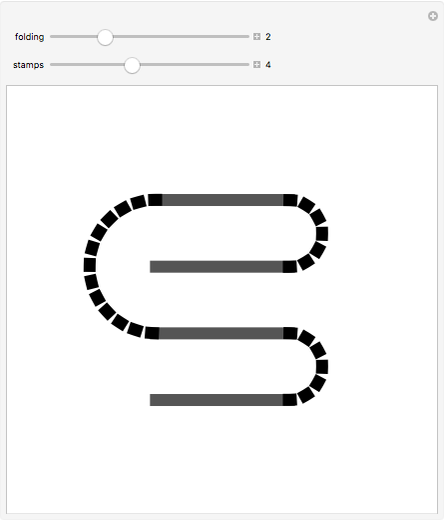
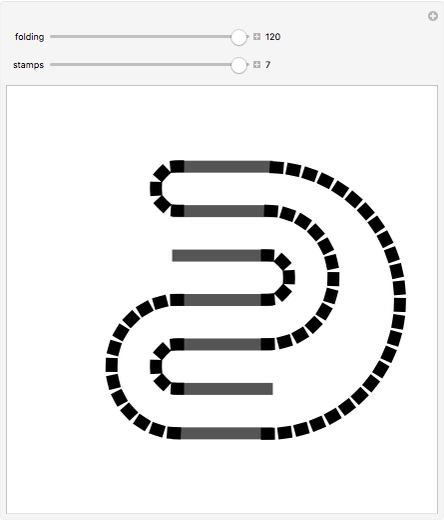
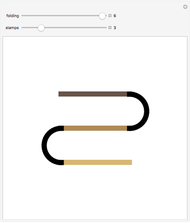
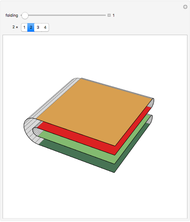
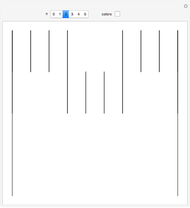
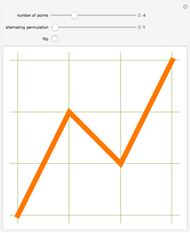
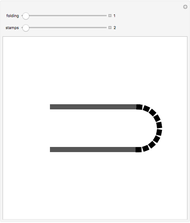
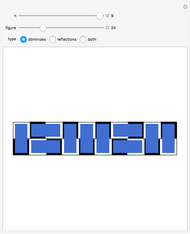
This Demonstration illustrates the different ways a strip of  unlabeled stamps can be folded into a stack one stamp wide. In each figure, the solid lines represent the stamps and the dotted lines represent the perforation between adjacent stamps.
unlabeled stamps can be folded into a stack one stamp wide. In each figure, the solid lines represent the stamps and the dotted lines represent the perforation between adjacent stamps.
Contributed by: Robert Dickau (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
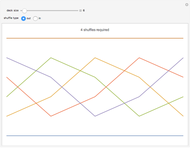
Snapshot 1: with more than one stamp, the number of unlabeled stamp foldings is less than  , the number of permutations of
, the number of permutations of  items; even with
items; even with  , unlabeled foldings are identical regardless of which stamp is on the top of the stack
, unlabeled foldings are identical regardless of which stamp is on the top of the stack
Snapshots 2 and 3: for  stamps, the number of labeled stamp foldings is less than
stamps, the number of labeled stamp foldings is less than  , since many permutations lead to impossible foldings
, since many permutations lead to impossible foldings
For example,  is an impossible folding, since the perforation joining stamps 1 and 2 would intersect the perforation joining 3 and 4. In addition, for unlabeled stamps, a folding that would be valid for labeled stamps could be identical to up to three other foldings, taking into account left-to-right reflections, top-to-bottom reflections, or both.
is an impossible folding, since the perforation joining stamps 1 and 2 would intersect the perforation joining 3 and 4. In addition, for unlabeled stamps, a folding that would be valid for labeled stamps could be identical to up to three other foldings, taking into account left-to-right reflections, top-to-bottom reflections, or both.
For more information, see Sequence A001011 in "The On-Line Encyclopedia of Integer Sequences."
Reference
[1] M. Gardner, "The Combinatorics of Paper Folding," in Wheels, Life and Other Mathematical Amusements, New York: W. H. Freeman, 1983 pp. 60–61.
Permanent Citation