Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Hurst Exponent of Stock Price

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The Hurst exponent is used as a measure of long-term memory of a time series [1]. If , there is white noise (i.e. there is no memory for the time series or, more technically, the random walk). The larger the value of , the more the time series has some type of memory.

[more]

This Demonstration uses a rescale range [2] to calculate the Hurst exponent of a stock price to show how days of earnings tend to have long-term memory. The larger the value of , the higher the exponent tends to be.

The parameter gathers days' accumulated earnings in the stock market. If we use to indicate the day's stock value, then days' accumulated earnings are .

This Demonstration shows four graphs:

1. stock prices of the company 2. quantile plot of days' accumulated earnings 3. histogram of days' earnings 4. estimation of the Hurst exponent line

The coefficient of in the last graph should be the Hurst exponent value.

[less]

Contributed by: Yushi Wang (January 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

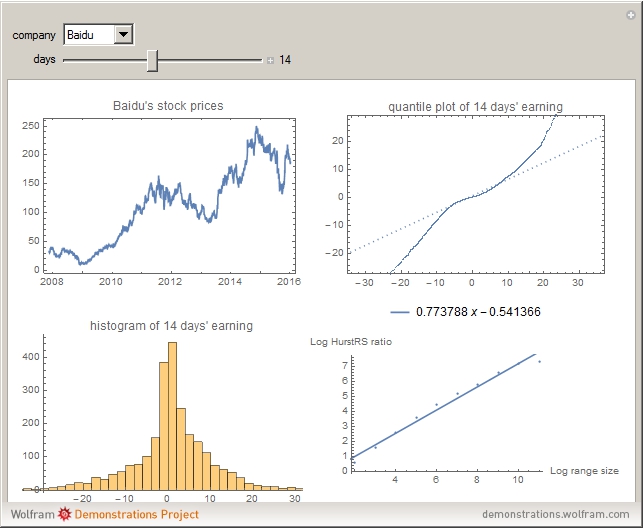
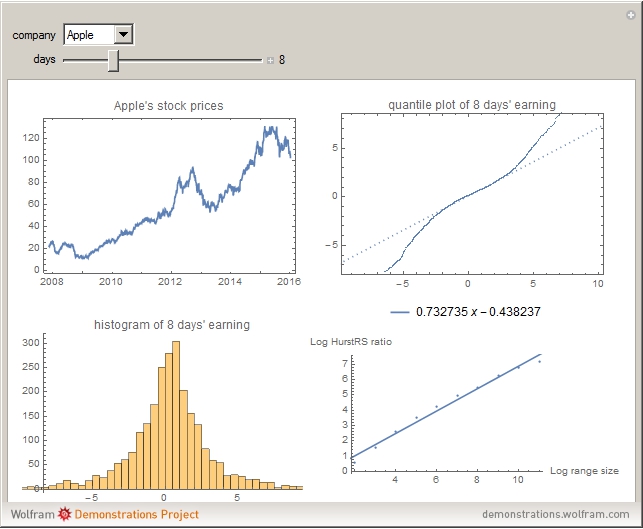
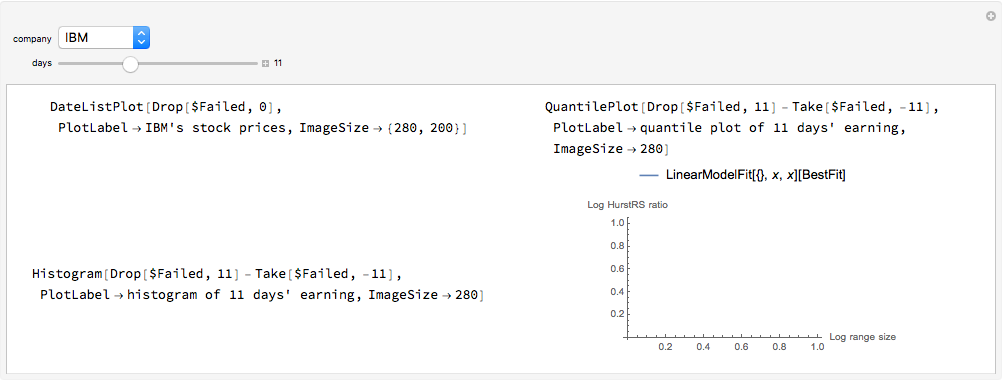
To calculate rescale range [2], calculate days' market returns with values . The HurstR function calculates the range of the values (max-min). HurstS gives the standard deviation of the values. HurstRS is the range divided by the standard deviation.

For the whole sequence , we can calculate a HurstRS value of the whole range, and we do the same by splitting the sequence into two parts and to calculate the HurstRS of the two ranges and average them. Then we repeat iteratively for four parts, eight parts, etc. until the range is small enough.

When we get all the HurstRS values of different range scales, we can plot them on a log-log plot of the range sizes and their HurstRS values, then do a linear model fit to the data, so that the slope of the line is the estimated Hurst exponent of the data.

References

[1] Wikipedia. "Hurst Exponent." (Jan 6, 2016) en.wikipedia.org/wiki/Hurst_exponent.

[2] Wikipedia. "Rescaled Range." (Jan 6, 2016) en.wikipedia.org/wiki/Rescaled_range.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send