Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Impulse Response and Transfer Function of a Raised Cosine Filter

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

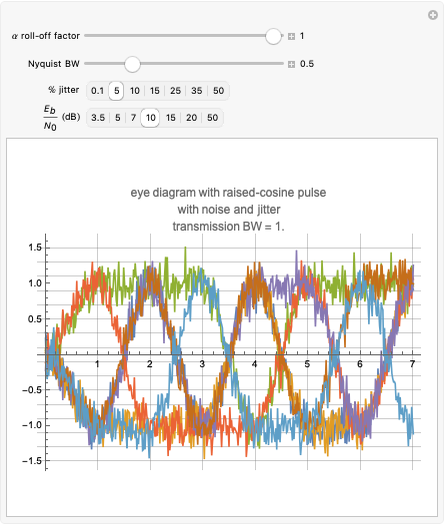
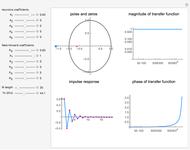
Intersymbol interference (ISI) occurs in digital communication systems when the symbols or bits of a digital signal overlap with adjacent symbols in time, distorting the received signal. ISI leads to an increase in the bit error rate of the system.

[more]

One way to mitigate ISI is through pulse shaping. Pulse shaping involves designing a filter that modifies the transmitted signal in such a way that the time domain zero-crossing of the received pulse aligns with the symbol boundaries.

The focus of this Demonstration is a specific pulse-shaping technique that results in a raised cosine pulse in the receiver. By adjusting the roll-off factor of the raised cosine pulse, you can observe its characteristics in both the time and frequency domains.

This Demonstration showcases the zero-crossing property of the raised cosine pulse, which remains invariant for all values of the roll-off factor. This property ensures that the pulse aligns with the symbol boundaries, reducing ISI.

[less]

Contributed by: Victor S. Frost (August 25)
(University of Kansas)
Open content licensed under CC BY-NC-SA

Details

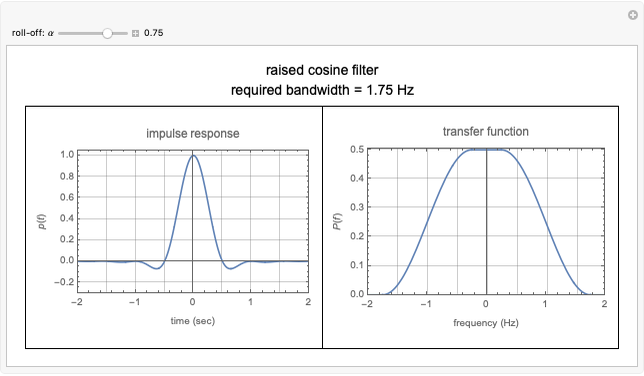
ISI can be mitigated using pulse shaping. Adjusting the end-to-end system to have an approximate raised cosine impulse response is a common method to control ISI. The frequency response and the time domain shape of a raised cosine pulse, that is, impulse response of a raised cosine filter, are given by [1]:

and

.

Here is the Nyquist bandwidth and is the roll-off factor.

In this Demonstration, the Nyquist bandwidth .

References

[1] S. Haykin and M. Moher, Introduction to Analog and Digital Communications, 2nd ed., Hoboken, NJ: Wiley, 2012.

[2] L. W. Couch, Digital and Analog Communications Systems, 7th ed., Upper Saddle River, NJ: Pearson/Prentice Hall, 2007.

[3] V. S. Frost. "Introduction to Communication Systems: An Interactive Approach Using the Wolfram Language." University of Kansas Libraries. (Jul 5, 2023) kuscholarworks.ku.edu/bitstream/handle/1808/31779/Introduction-to-Communication-Systems-Deployed-V3.cdf?sequence=5&isAllowed=y.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send