Second-Order Digital Filter Design

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
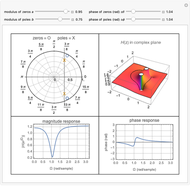
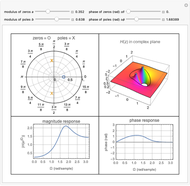
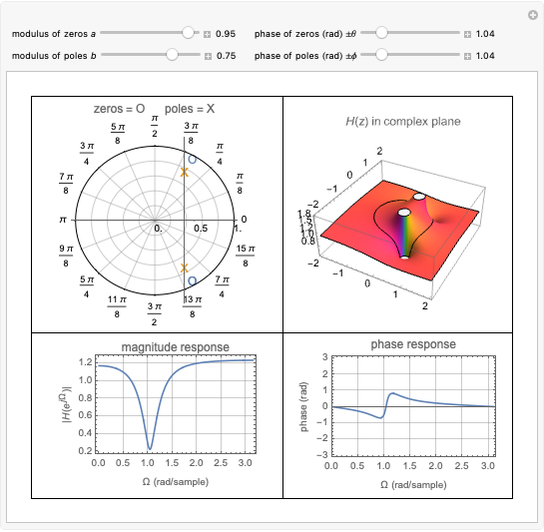
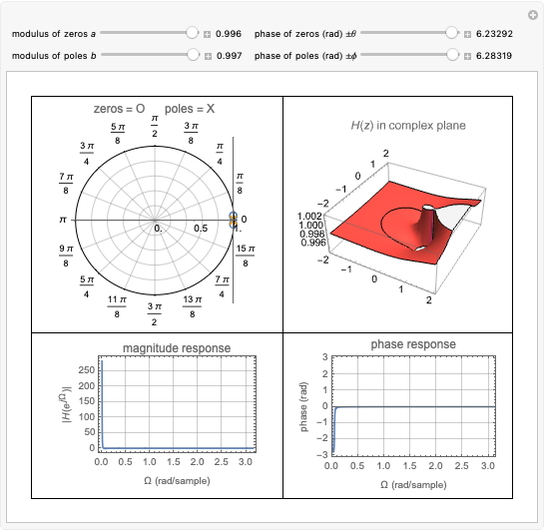
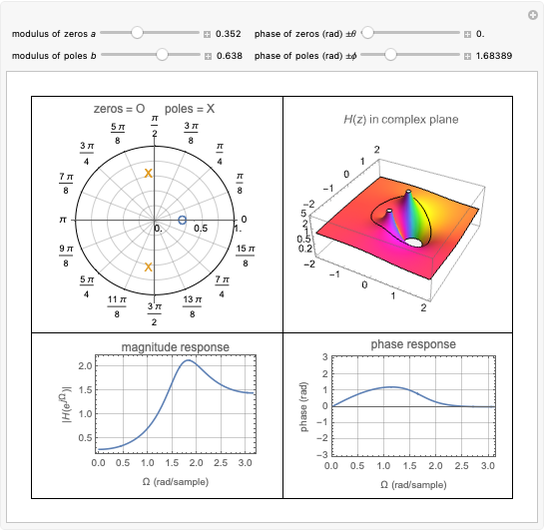
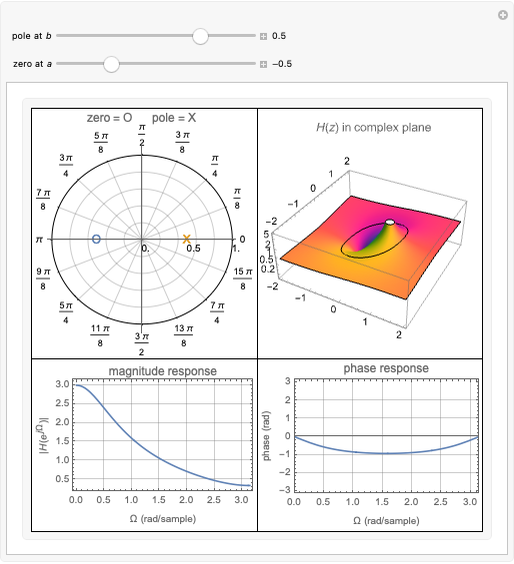
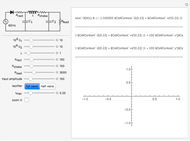
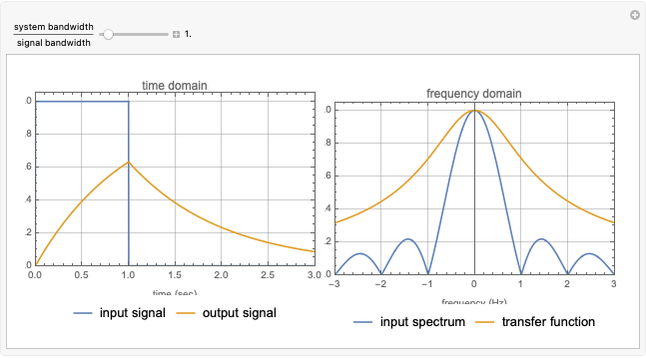
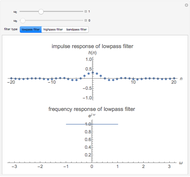
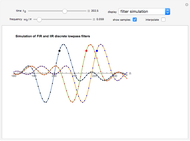
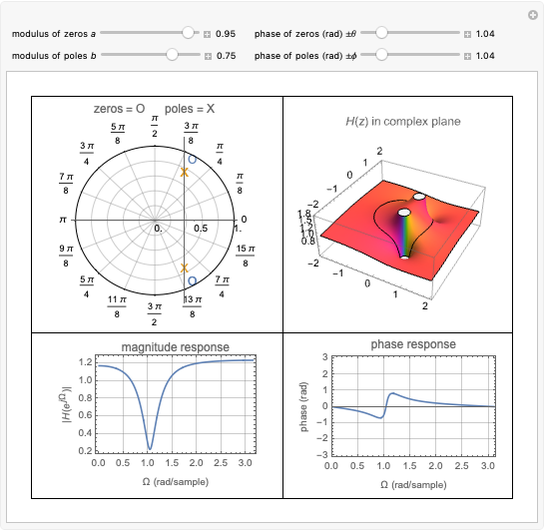
This Demonstration considers the design of a second-order digital filter. Multiple perspectives of the system are shown, including the placement of poles and zeros, a 3D plot of the transfer function in the  domain with a highlighted unit circle and the filter magnitude and phase responses. The relationships between the locations of poles or zeros, the frequency response and the 3D plot of
domain with a highlighted unit circle and the filter magnitude and phase responses. The relationships between the locations of poles or zeros, the frequency response and the 3D plot of  are also shown. The transfer function is presented in its general form, along with the corresponding difference equation for the given placement of the poles and zeros. You can change their positions to see how they affect the lowpass, highpass and bandpass digital filters.
are also shown. The transfer function is presented in its general form, along with the corresponding difference equation for the given placement of the poles and zeros. You can change their positions to see how they affect the lowpass, highpass and bandpass digital filters.
Contributed by: Victor S. Frost (August 27)
(University of Kansas)
Open content licensed under CC BY-NC-SA
Details
Linear time-invariant (LTI) discrete-time systems are commonly described from different perspectives, including a difference equation and a transfer function  , where
, where  is a complex variable. The frequency response of the system can be obtained by evaluating
is a complex variable. The frequency response of the system can be obtained by evaluating  on the unit circle. To visualize this, a 3D plot of
on the unit circle. To visualize this, a 3D plot of 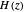 is shown, with the unit circle highlighted. You can see how the locations of the poles and zeros affect the behavior of the system.
is shown, with the unit circle highlighted. You can see how the locations of the poles and zeros affect the behavior of the system.
The transfer function is given by
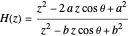 .
.
The difference equation is given by
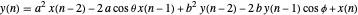 .
.
This Demonstration focuses on a specific scenario in which the poles are within the unit circle. This configuration ensures a bounded-input, bounded-output (BIBO) stable system. Showcasing different descriptions and representations leads to a better understanding of the performance and design of a first-order discrete-time system. You can vary the locations of the poles and zeros to show how a second-order system can be used as a lowpass, bandpass or highpass filter.
Reference
[1] F. T. Ulaby and A. E. Yagel, Signals and Systems: Theory and Applications, Michigan Publishing, 2018. (Jul 21, 2023) ss2.eecs.umich.edu.
Snapshots
Permanent Citation