Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

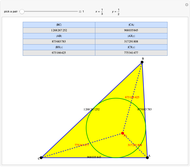
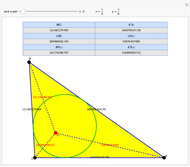
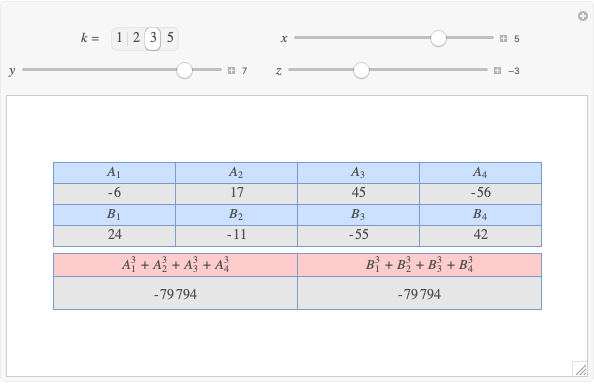
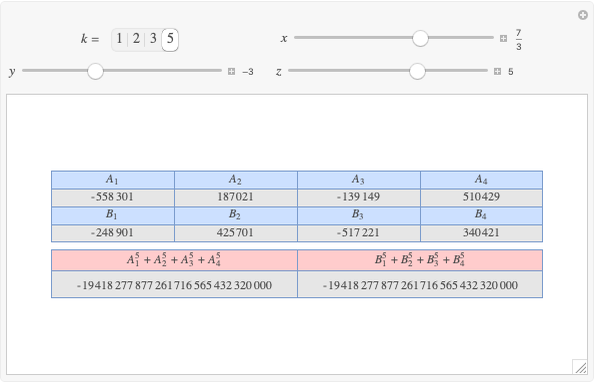
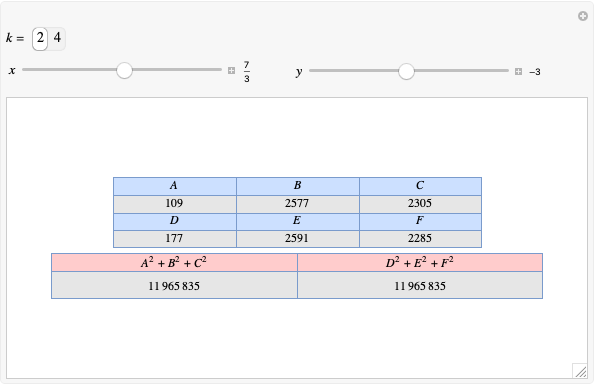
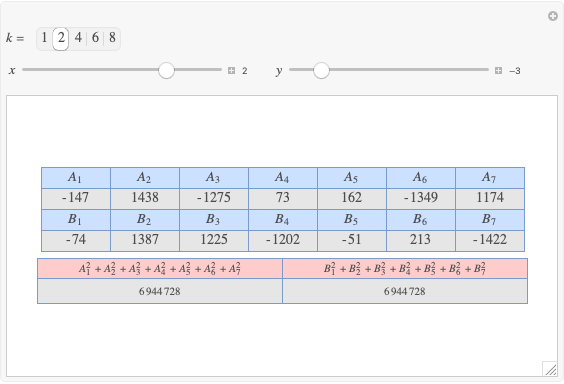
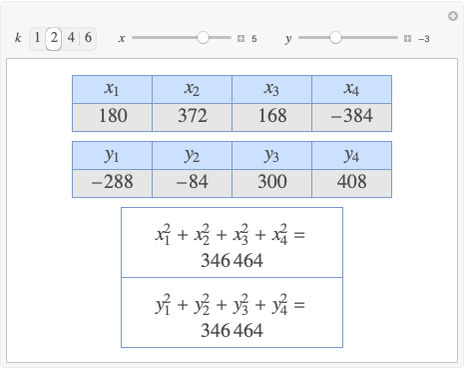
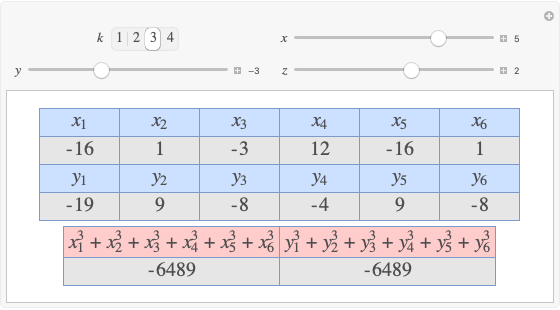
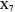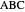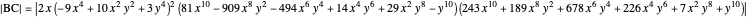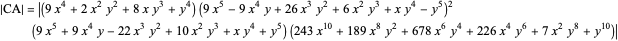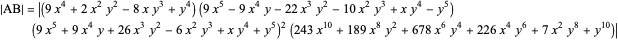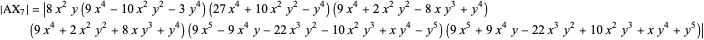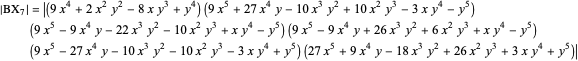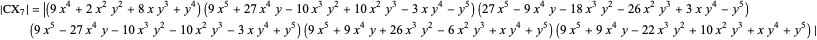Integer Triangle of the Gergonne Point

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

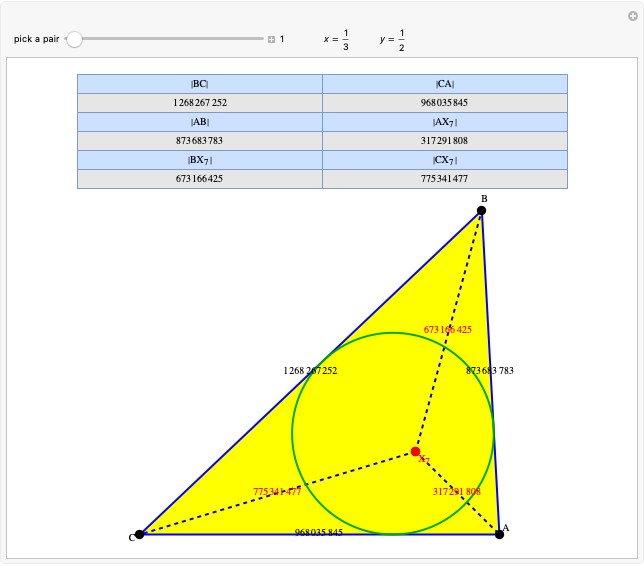
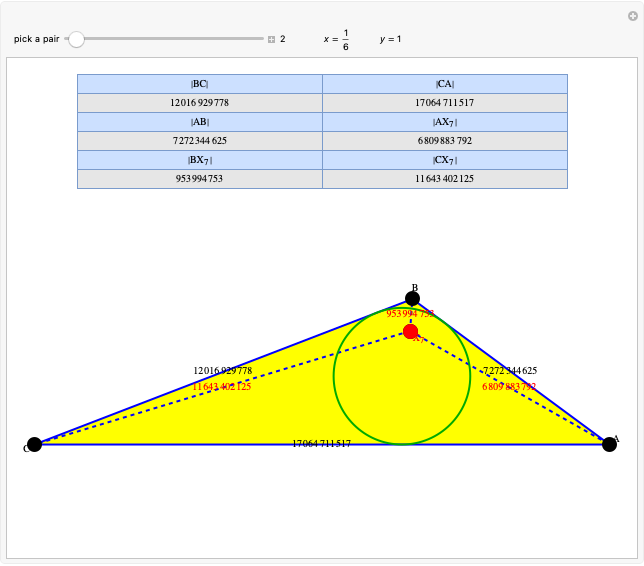
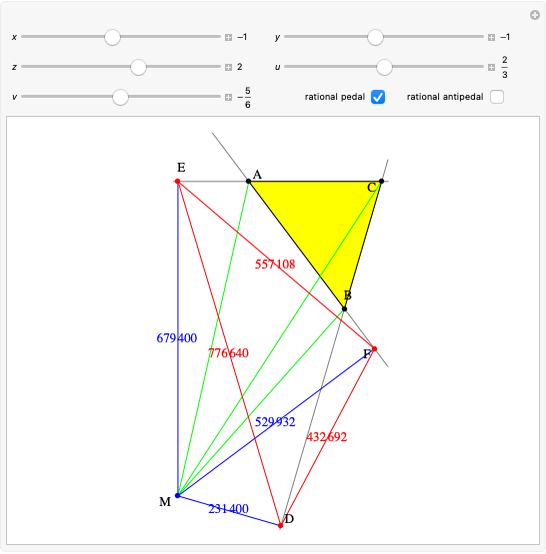
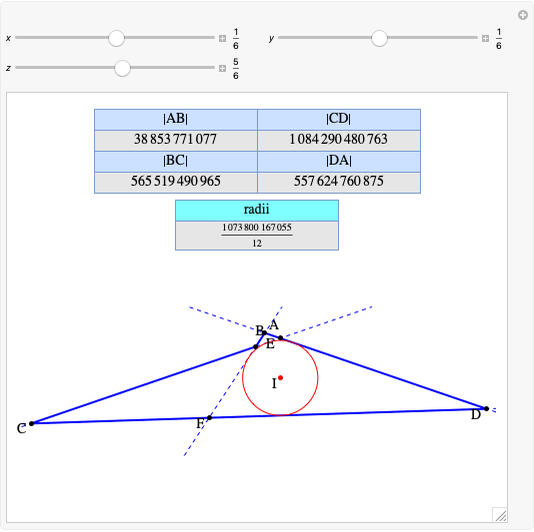
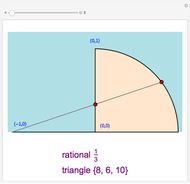
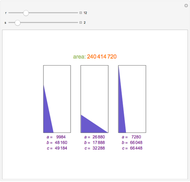
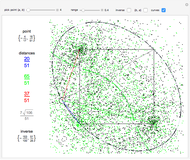
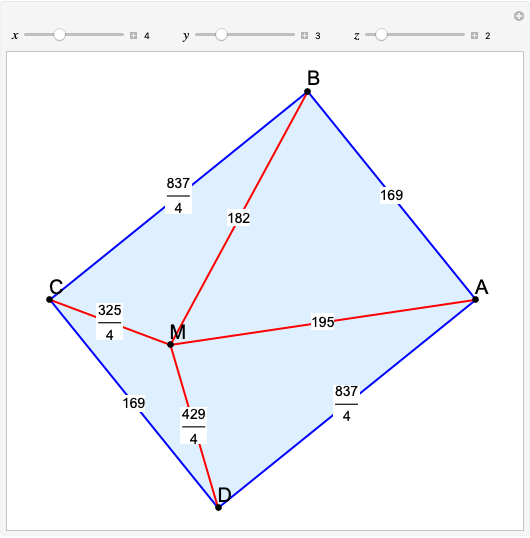
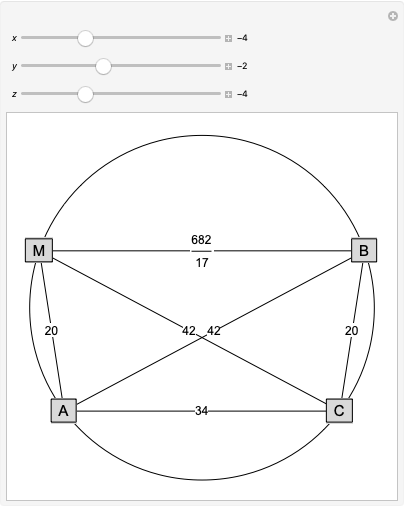
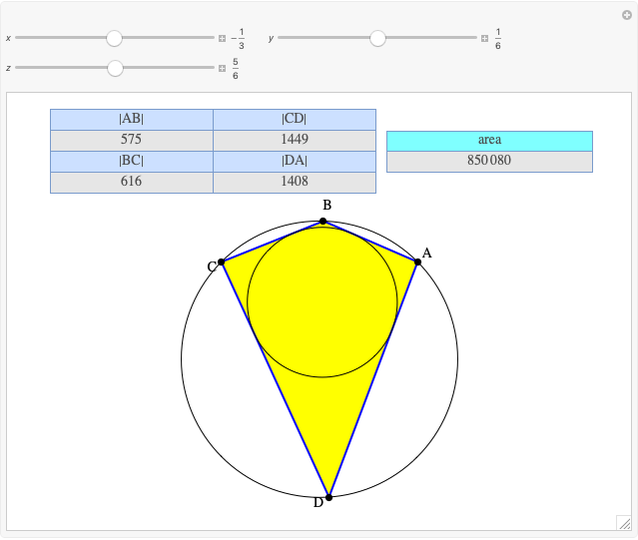
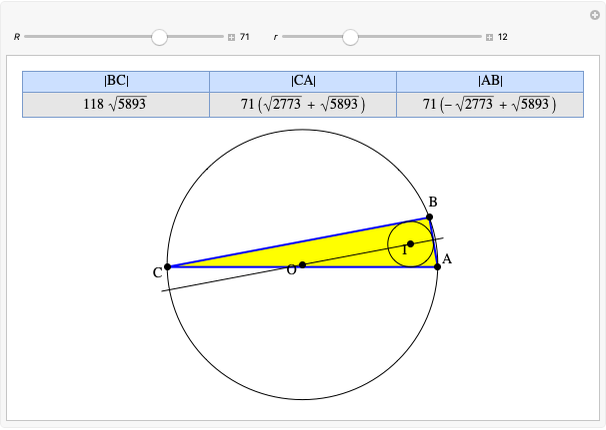
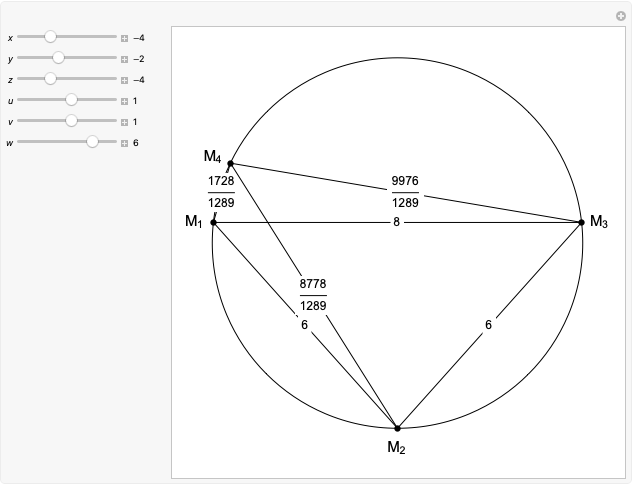
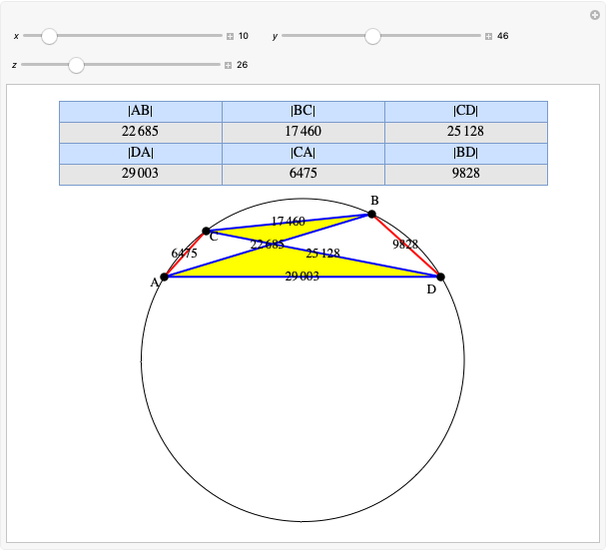
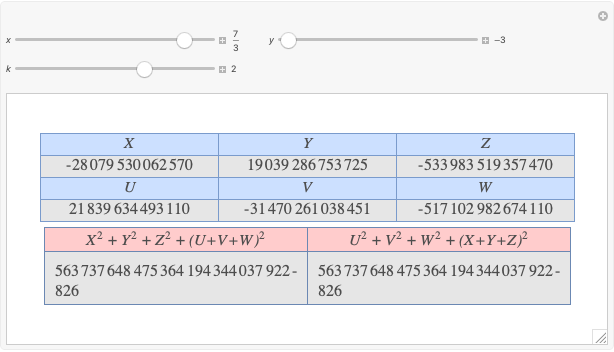
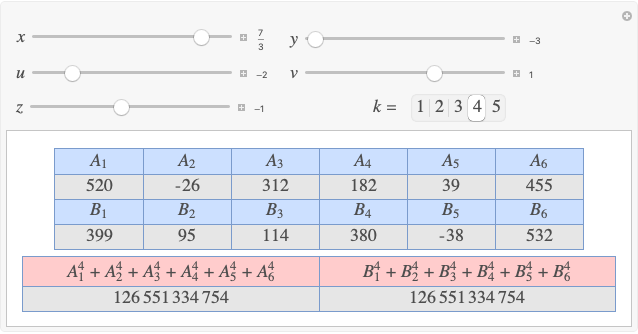
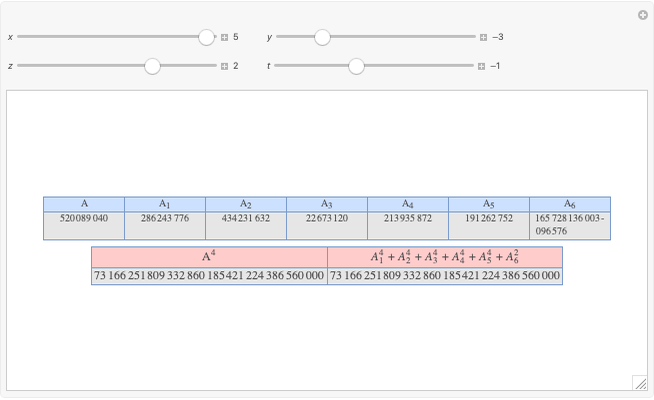
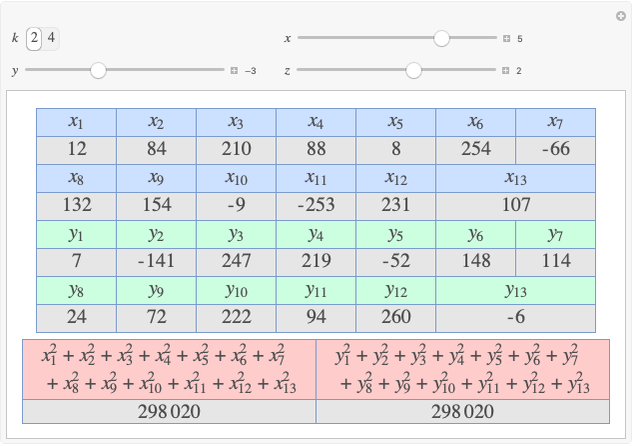
A rational triangle has all three sides rational numbers, and a rational point 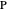with respect to a triangle means that the distances from 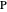to the vertices of are rational.

[more]

If and are rational and , it is possible to construct a rational triangle based on these values such that the Gergonne point is a rational point of [1].

Then we have:

According to the rational isogonal conjugates theorem, since is a rational point of , so is its isogonal conjugate .

[less]

Contributed by: Minh Trinh Xuan (June 13)
Open content licensed under CC BY-NC-SA

Details

Reference

[1] C. Kimberling. "Encyclopedia of Triangle Centers." (Dec 29, 2022) faculty.evansville.edu/ck6/encyclopedia.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send