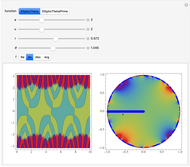
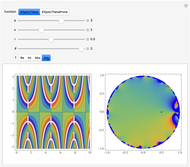
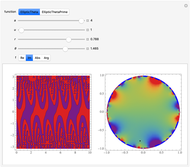
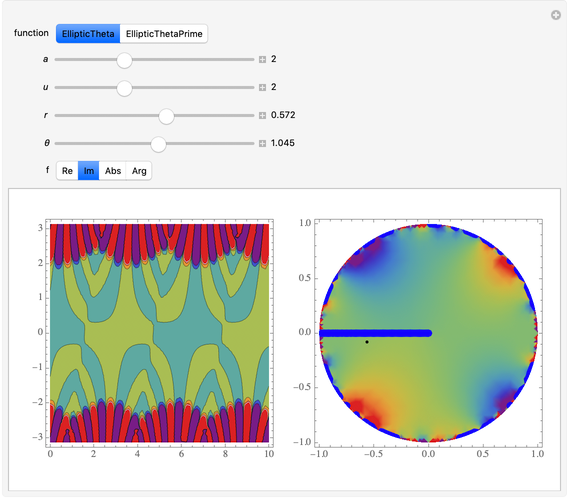
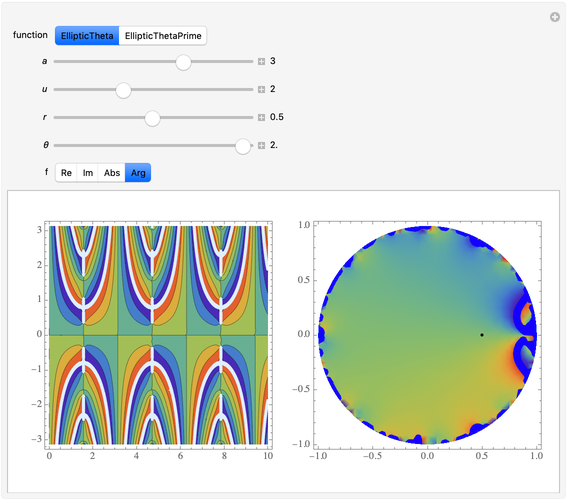
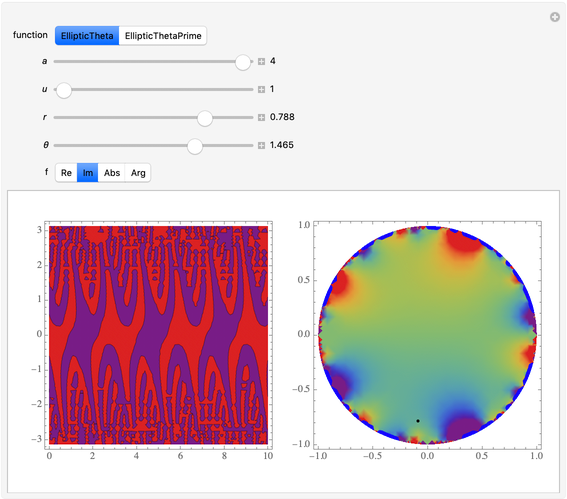
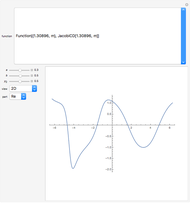
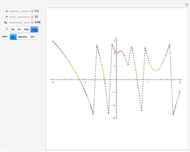
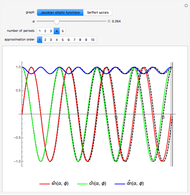
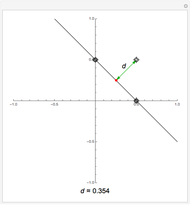
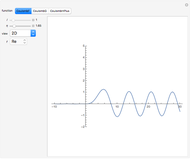
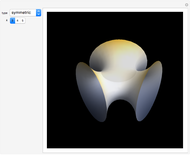
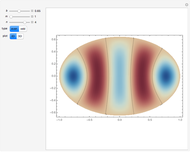
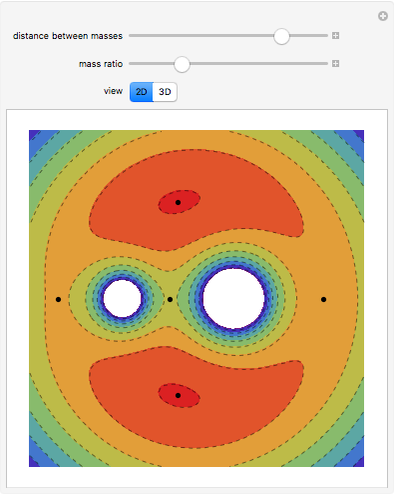
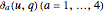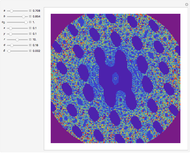
Theta functions are a family of special functions , important in number theory, analysis, heat conduction, representation of solitons, and quantum field theory. The plots show theta functions for complex and nome (a parameter used for elliptic functions) 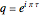(left) and for complex on the unit disk (right). The black dot in the graphic on the right indicates the point 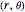. These functions are related to several other special functions: the Dedekind function, the Weierstrass elliptic functions, and the Riemann zeta function, with many identities connecting them [1, 2]. For a basic introduction to elliptic functions, see [3]; generalizations of theta functions include the Ramanujan theta functions.