Approximating the Jacobian Elliptic Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Jacobian elliptic functions are extensions and generalizations of trigonometric sine and cosine functions. Applications in physics abound. For example, the functions  and
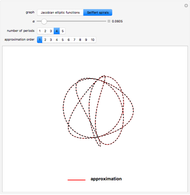
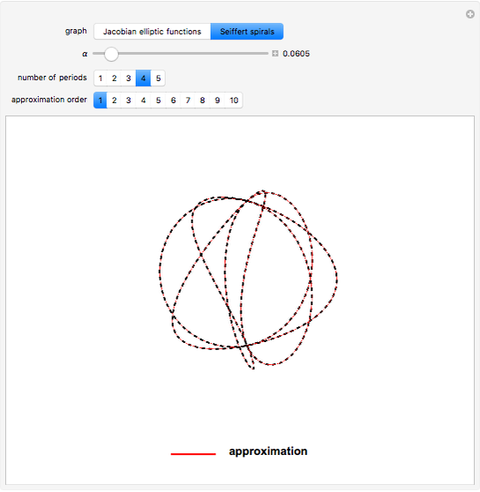
and  occur in the exact solution of the equations of motion for the plane pendulum [1]. Any approximation procedure to solve the pendulum equations of motion involves approximations to the Jacobian elliptic functions [2]. The approximation also pertains to Seiffert spirals [3], trajectories along the surface of a sphere.
occur in the exact solution of the equations of motion for the plane pendulum [1]. Any approximation procedure to solve the pendulum equations of motion involves approximations to the Jacobian elliptic functions [2]. The approximation also pertains to Seiffert spirals [3], trajectories along the surface of a sphere.
Contributed by: Brad Klee (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
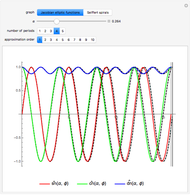
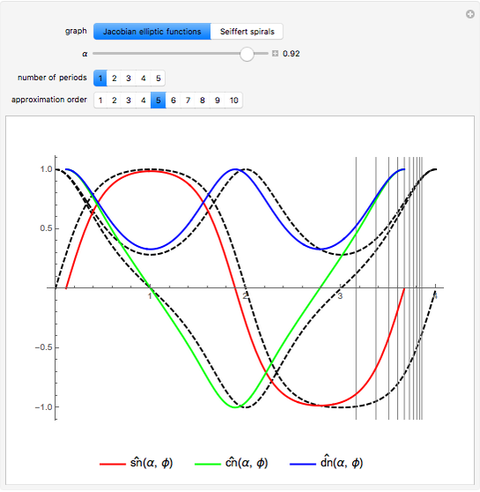
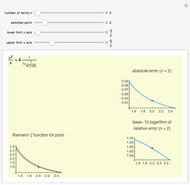
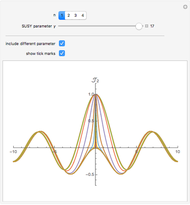
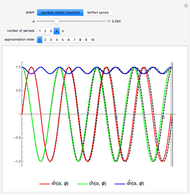
The  axis of the graphs for
axis of the graphs for  ,
,  , and
, and  is measured in units of
is measured in units of  , the complete elliptic integral of the first kind. The functions
, the complete elliptic integral of the first kind. The functions  ,
,  have period
have period  , while the function
, while the function  has period
has period  . The term-by-term expansion of
. The term-by-term expansion of  is given [4] by
is given [4] by
 .
.
Approximations of the Jacobian elliptic functions  ,
,  , and
, and  in parametric form follow from an arbitrary-precision solution of the plane pendulum's equations of motion [1, 3]:
in parametric form follow from an arbitrary-precision solution of the plane pendulum's equations of motion [1, 3]:
 ,
,
 ,
,
 ,
,
 ,
,
where  are the polar coordinates of phase space. The function
are the polar coordinates of phase space. The function  gives the relation between the angle
gives the relation between the angle  and the domain of the Jacobian elliptic functions,
and the domain of the Jacobian elliptic functions,  . The approximate phase radius and time dependence are:
. The approximate phase radius and time dependence are:
 ,
,
 ,
,
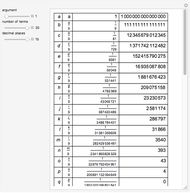
where the coefficients  and
and  are computable rational numbers with closed form as yet unknown (Cf. OEIS A273506, A274130 [5]).
are computable rational numbers with closed form as yet unknown (Cf. OEIS A273506, A274130 [5]).
In the complete limit, as  the approximation is exact. Choosing some finite
the approximation is exact. Choosing some finite  introduces error at order
introduces error at order  . One easy way to see the error is to consider the approximate period, which is directly proportional to the
. One easy way to see the error is to consider the approximate period, which is directly proportional to the  dependent factor:
dependent factor:
 .
.
In the plots, vertical lines show convergence toward the exact period as  increases; however, cumulative errors always become evident if the function domain or time chosen is large enough. Convergence depends strongly on the chosen value of
increases; however, cumulative errors always become evident if the function domain or time chosen is large enough. Convergence depends strongly on the chosen value of  .
.
For definitions of the Seiffert spirals see the wonderful article by Erdös [3].
References
[1] A. J. Brizard, "A Primer on Elliptic Functions with Applications in Classical Mechanics." arxiv.org/abs/0711.4064.
[2] B. Klee, "Plane Pendulum and Beyond by Phase Space Geometry." arxiv.org/abs/1605.09102.
[3] P. Erdös, "Spiraling the Earth with C. G. J. Jacobi," American Journal of Physics 68, 2000 pp. 888–895. doi:10.1119/1.1285882.
[4] M. Abramowitz and I. A. Stegun. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. people.math.sfu.ca/~cbm/aands/page_591.htm.
[5] The OEIS Foundation. The Online Encyclopedia of Integer Sequences. A273506, A273507, A274130, A274131, A274076, A274078.oeis.org.
Permanent Citation