Jiles-Atherton Model of Magnetic Hysteresis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
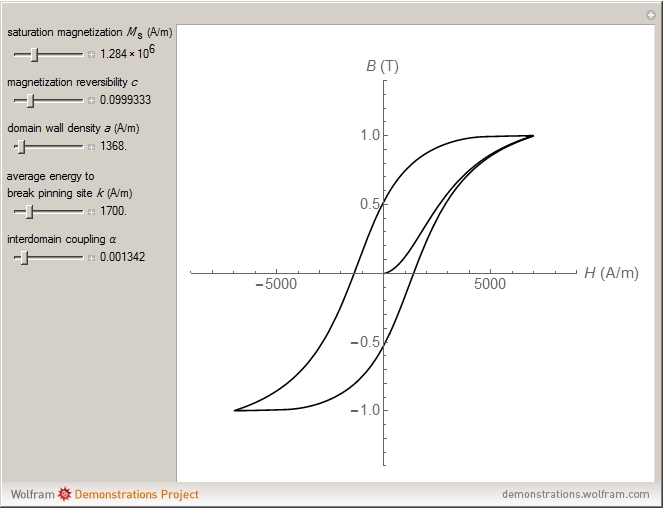
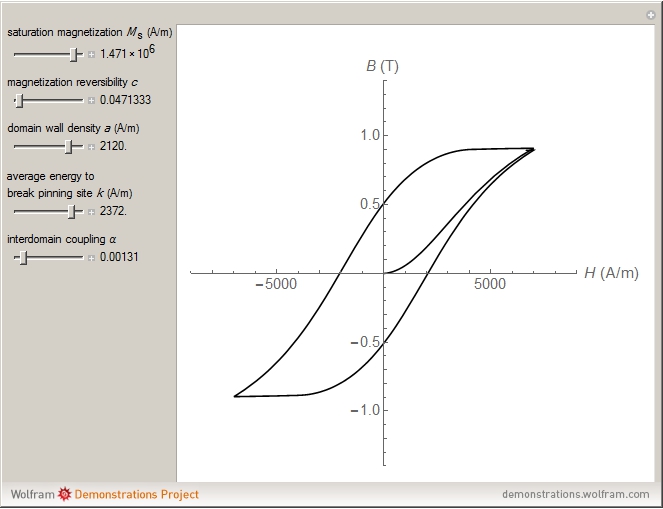
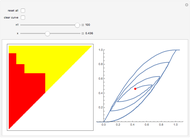
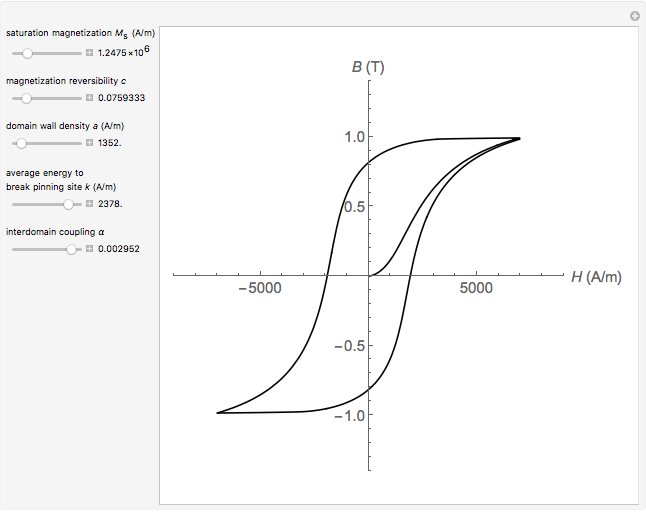
The Jiles–Atherton model of magnetic hysteresis is used to calculate minor and major hysteresis loops from physical parameters of isotropic magnetic materials. Five parameters are considered:  (saturation magnetization),
(saturation magnetization),  (magnetization reversibility),
(magnetization reversibility),  (average energy to break pinning site),
(average energy to break pinning site),  (domain wall density) and
(domain wall density) and  (interdomain coupling). You can vary them with sliders. The graphic shows the plot of
(interdomain coupling). You can vary them with sliders. The graphic shows the plot of  (in tesla) versus
(in tesla) versus  (in amperes/meter).
(in amperes/meter).
Contributed by: Santosh Kumar and Tarun Tummuru (December 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
One of the first attempts to model magnetic hysteresis can be traced back to Langevin in 1905, who initially developed the theory for paramagnetic materials that was later extrapolated to ferromagnetic materials. The defining relation involves the Langevin function, which describes the saturation phenomenon. Improved semi-empirical models to explain hysteresis behavior were subsequently proposed by Presaich and by Jiles and Atherton (J–A) [1].
The J–A model uses a macroscopic picture in which the fundamental idea is to counteract magnetization by anhysteretic behavior represented by a sigmoidal curve. Hysteresis can be understood as the result of energy dissipation on voids, inclusions and dislocations of crystalline structure (called pinning sites).
References
[1] D. C. Jiles and D. L. Atherton, "Theory of Ferromagnetic Hysteresis," Journal of Magnetism and Magnetic Materials, 61(1–2), 1986 pp. 48–60. doi:10.1016/0304-8853(86)90066-1.
[2] M. F. Jaafar and M. A. Jabri, "Study and Modeling of Ferromagnetic Hysteresis," in Electrical Engineering and Software Applications (ICEESA), 2013 International Conference on Electrical Engineering and Software Applications, Hammamet, Tunisia, 2013, New York: IEEE, 2013 pp. 1–6. doi:10.1109/ICEESA.2013.6578426.
Permanent Citation