Magnetic Field and Magnetic Induction in a Cylindrical Bar Magnet

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
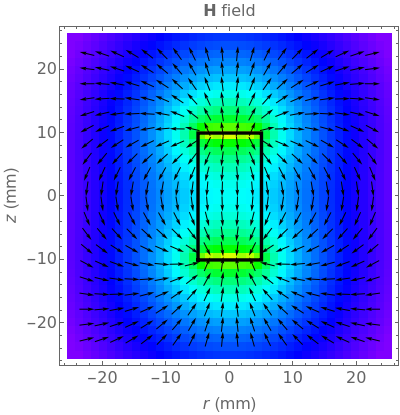
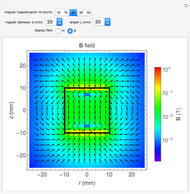
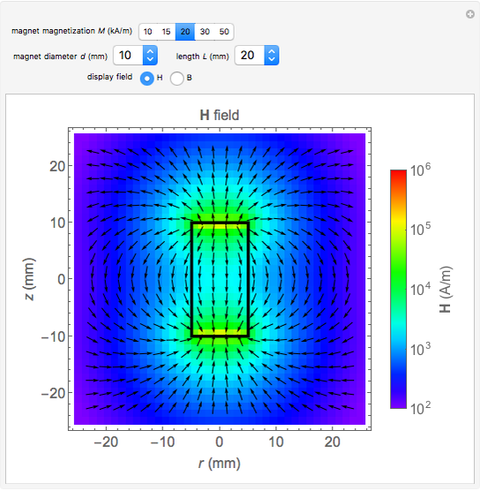
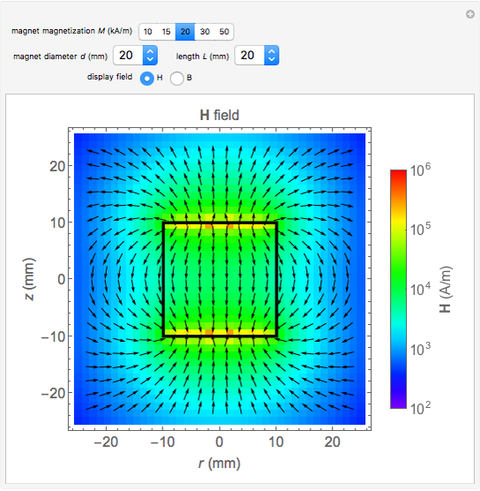
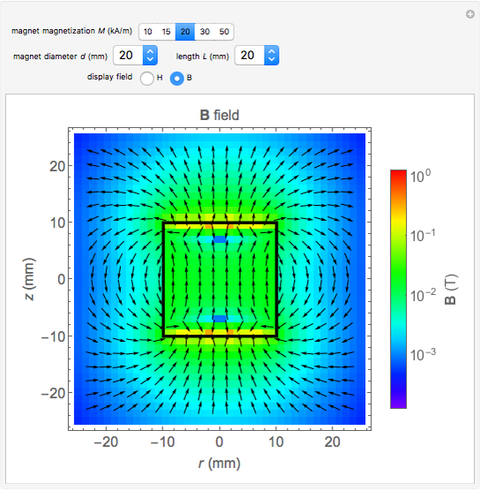
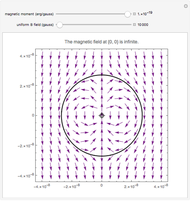
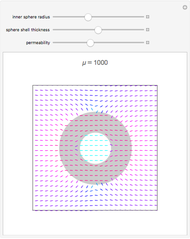
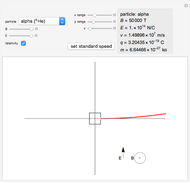
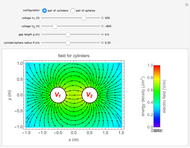
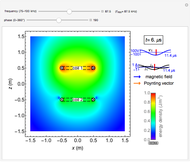
This Demonstration shows the quantitative magnetic field and magnetic induction for a cylindrical bar magnet. The magnetization  is assumed to be in the
is assumed to be in the  direction and uniform within a magnet of diameter
direction and uniform within a magnet of diameter  and length
and length  . Colors on a logarithmic scale show field intensity and arrows show its direction. The field
. Colors on a logarithmic scale show field intensity and arrows show its direction. The field  and induction
and induction  outside the magnet satisfy
outside the magnet satisfy  , so the field patterns are identical (the same color is used for both fields). They are different inside the magnet, since there
, so the field patterns are identical (the same color is used for both fields). They are different inside the magnet, since there  . While
. While  vectors go from the north pole to the south pole (top to bottom) in all regions,
vectors go from the north pole to the south pole (top to bottom) in all regions,  vectors return to the north pole through the magnetized body.
vectors return to the north pole through the magnetized body.
Contributed by: Y. Shibuya (September 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
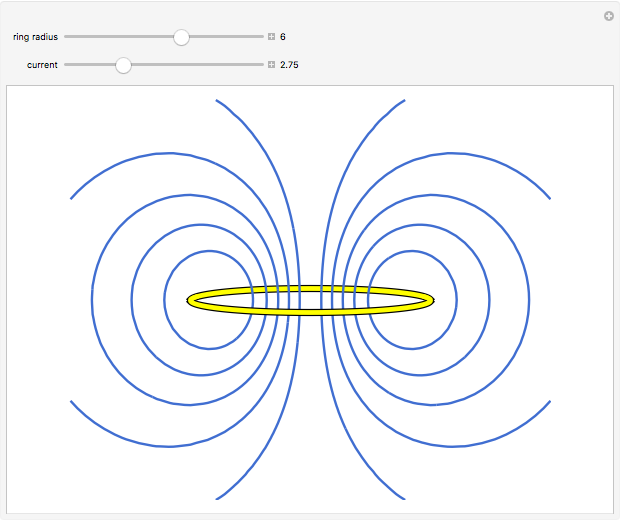
The magnetic field can be regarded as originating from two parallel, oppositely charged monopolar disks situated at the ends of the magnet. Since the effective surface magnetic charge densities are equal to
 , the magnetic field of any point in the
, the magnetic field of any point in the  -
- plane, a 2D vector, can be calculated by integrating on those surfaces:
plane, a 2D vector, can be calculated by integrating on those surfaces:
 .
.
Mathematica finds a function after integrating with respect to  (i.e. in radial direction) that can be written as:
(i.e. in radial direction) that can be written as:
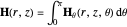 .
.
Snapshot 1: example of  field; all vectors go from north pole to south pole
field; all vectors go from north pole to south pole
Snapshot 2 : example of  field; vectors circulate between north pole and south pole
field; vectors circulate between north pole and south pole
Snapshot 3 : example of  field of thin bar magnet; the field resembles that of two point charges
field of thin bar magnet; the field resembles that of two point charges
Permanent Citation