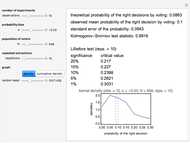
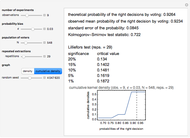
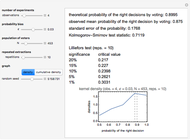
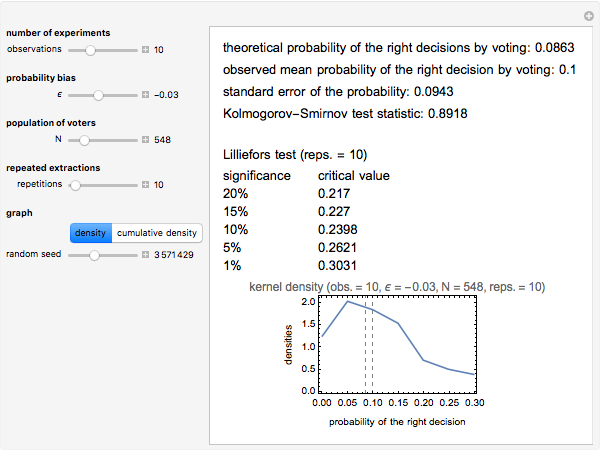
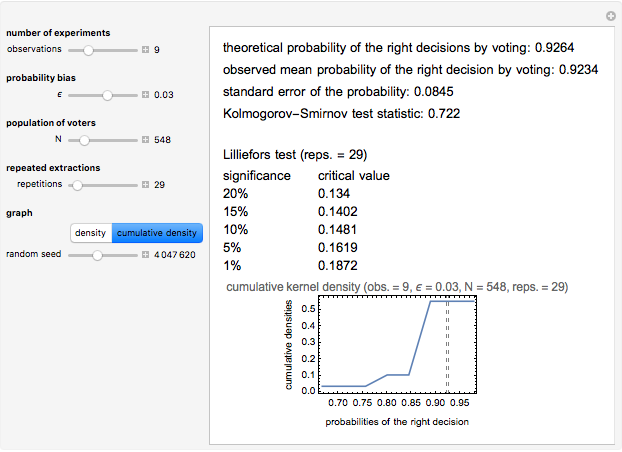
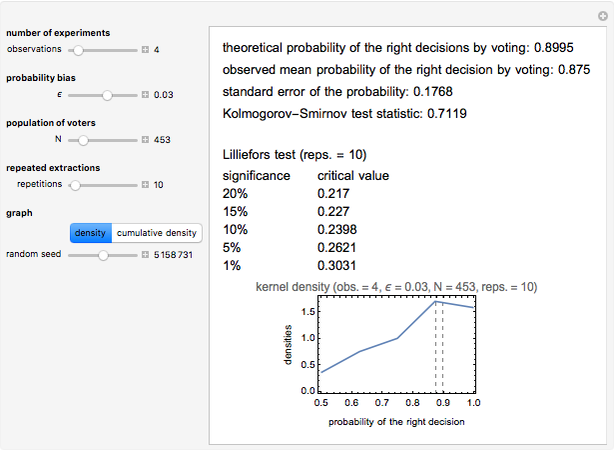
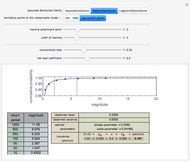
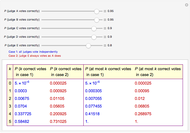
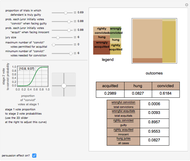
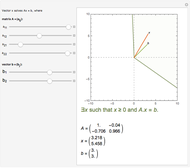
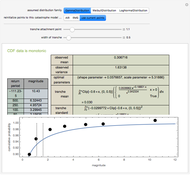
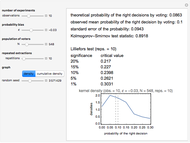
This is the fifth of five Demonstrations about Condorcet's jury theorem (1785). Here we show estimates of kernel density and cumulative kernel density functions for a given probability bias and number of voters —compare with Parts 3 and 4 in this series of Demonstrations (see Related Links). We test the goodness of fit of the observed right decision probabilities to normality. For reference, the test statistic table for the Lilliefors normality test is presented (the test statistic and null hypothesis are the same as the Kormogorov–Smirnov test for normality). The critical values presented are based on Abdi and Molin [1]; see their summary for the details of the test. Note also the Gaussian kernel is used in the kernel estimation.