Convergence of Probability II: Condorcet's Jury Theorem, Part 4
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
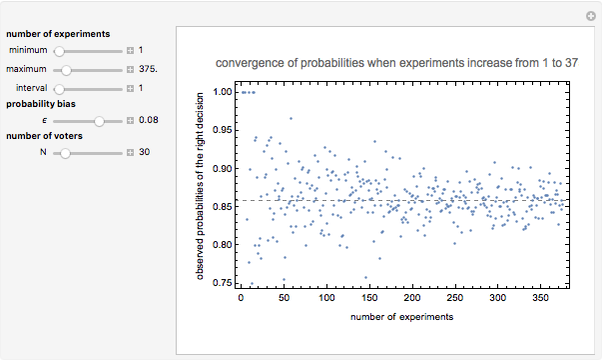
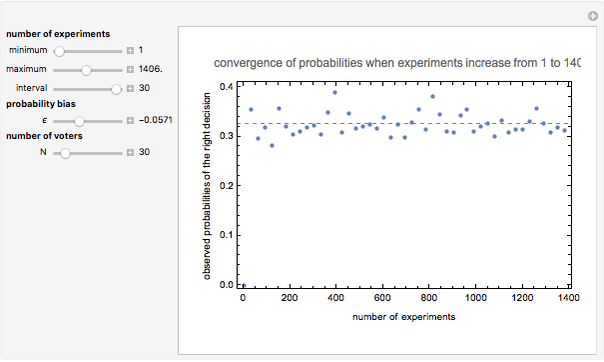
This is the fourth of five Demonstrations about Condorcet's jury theorem (1785). For a given probability bias 
and number of voters 
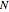, the probability that an election yields the "correct" result can be calculated from the binomial distribution and is shown on the plot as a horizontal dashed line. As the number of elections grows, the fraction of elections yielding the "correct" result approaches this value.
Contributed by: Tetsuya Saito (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration shows the convergence of probability to a certain probability for a given number of voters as the number of experiments increases. The difference from another Demonstration in this series (Convergence of Probability I) is as follows: In the former Demonstration, we examined convergence of probability as the number of voters increases with a given number of experiments. Then we could find the probability of correct decision converges to 1 as the number of voters increases. In this Demonstration, in turn with a given number of voters, we verify the convergence of probability to a certain number as the number of experiments increases, as indicated by the theoretical model.
Convergence of Probability I: Condorcet's Jury Theorem, Part 3
Tetsuya Saito
Theoretical Model: Condorcet's Jury Theorem, Part 1
Tetsuya Saito
Vote for Justice: Condorcet's Jury Theorem, Part 2
Tetsuya Saito
Kernel Density Estimations: Condorcet's Jury Theorem, Part 5
Tetsuya Saito
Moral Hazard and Least-Cost Contracts: Impact of Changes in Conditional Probabilities
Randy Silvers (Deakin University)
Europe Vote Exponent
Michael Schreiber
Iterated Games
Seth Chandler
Property Coinsurance
Seth J. Chandler
Tax Rates and Tax Revenue
Seth J. Chandler
Bilateral Accident Model
Seth J. Chandler
-
Theoretical Model: Condorcet's Jury Theorem, Part 1
Tetsuya Saito -
Kernel Density Estimations: Condorcet's Jury Theorem, Part 5
Tetsuya Saito -
Convergence of Probability II: Condorcet's Jury Theorem, Part 4
Tetsuya Saito -
Convergence of Probability I: Condorcet's Jury Theorem, Part 3
Tetsuya Saito -
Vote for Justice: Condorcet's Jury Theorem, Part 2
Tetsuya Saito -
Farkas's Lemma in Two Dimensions
Tetsuya Saito