Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Lion and Man

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

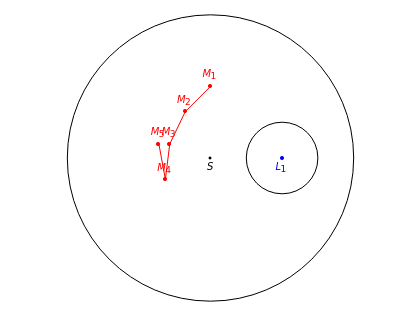
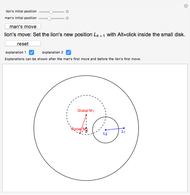
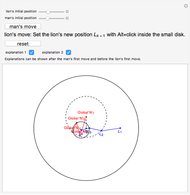
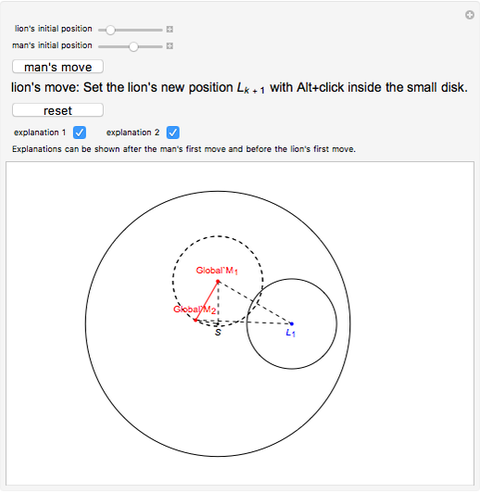
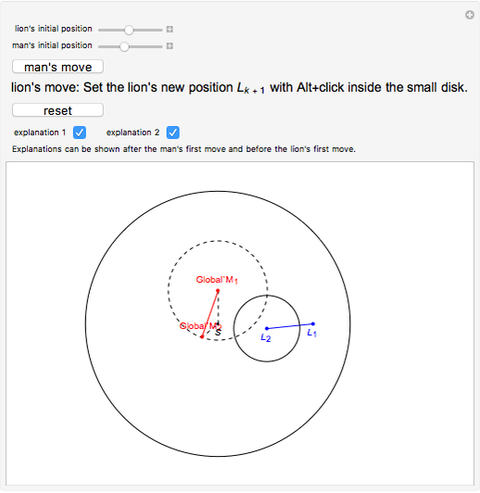
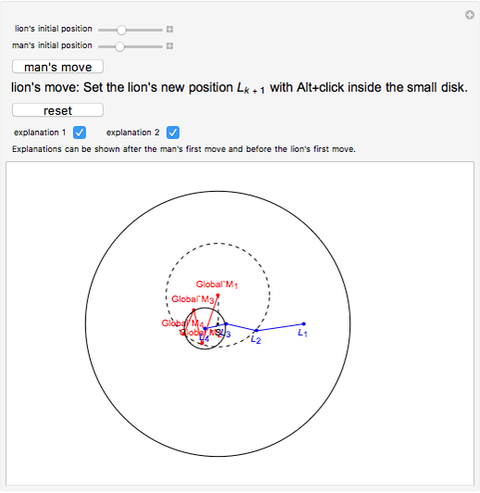
A man and a lion are inside a disk of radius 1 with center . Both have a top speed of 1. Can the man choose a strategy to avoid being captured by the lion?

[more]

To use the Demonstration, alternate the man's move (button) and the lion's move (choose a point inside the small circle and Alt+click).

A solution consists of a polygonal line of length , with , where . The lion can run a path of the same length and can choose the strategy so that the distance converges to 0, but only as time goes to infinity.

The man's strategy is as follows. The point is constructed toward the center of the disk so that the segment is of length and perpendicular to . The square of the distance of to the center of the disk is

So the man is always inside the disk (explanation 1 for ).

The distance between the man and the lion is (explanation 2 for ).

[less]

Contributed by: Izidor Hafner (April 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

To prove the construction is correct, it is necessary to show that the distance of to is less than 1 and that the length of is greater than 0.

References

[1] J. E. Littlewood, A Mathematician's Miscellany (Russian edition), Moscow: Nauka, 1973 pp. 141–143.

[2] V. Devide, 100 Elementary but Difficult Problems (in Croatian), Belgrade: ZIUSRS, 1965 pp. 87–89.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send