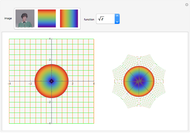
Mapping Contour Integrals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
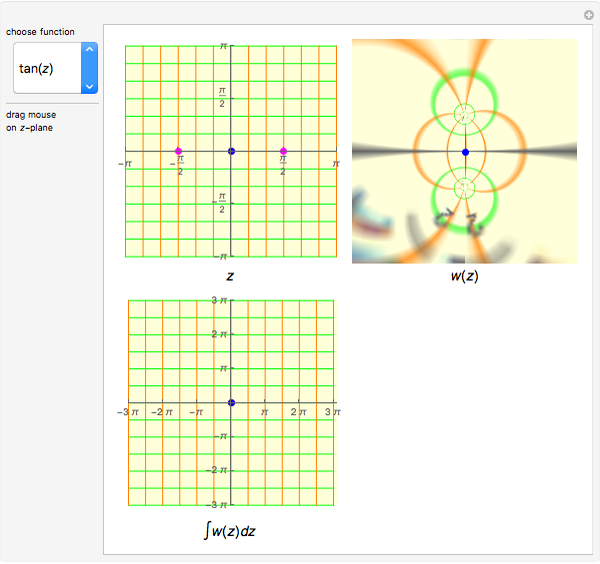
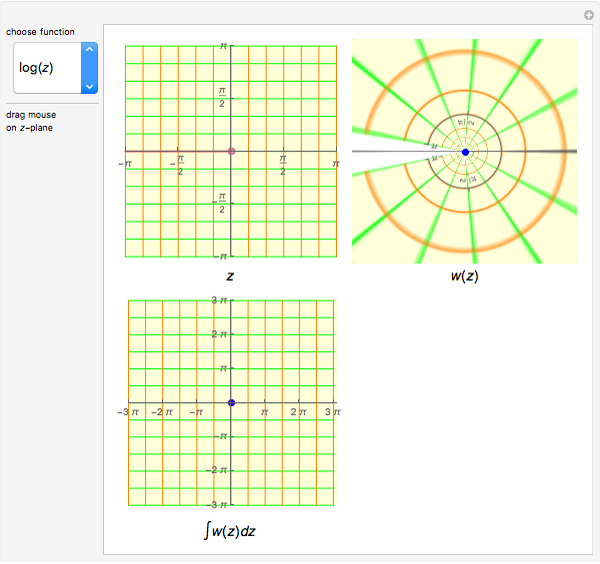
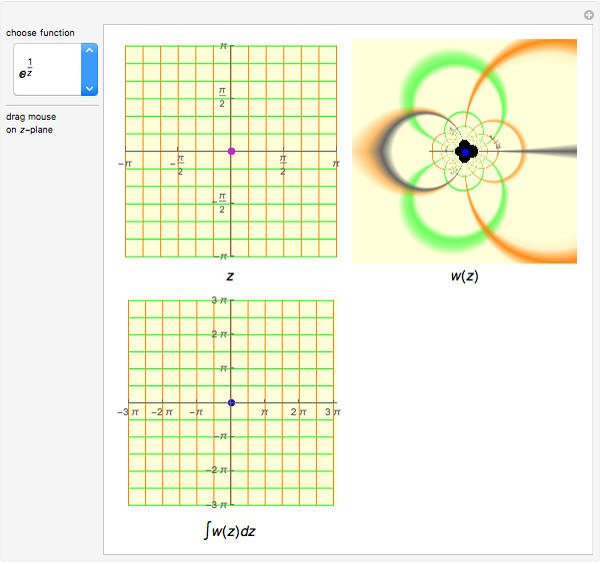
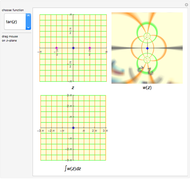
This Demonstration shows the paths of contour integrals over some basic complex functions.
[more]
Contributed by: Hayashi Yoshiaki (July 2017)
Open content licensed under CC BY-NC-SA
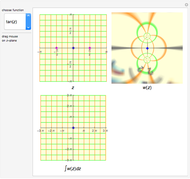
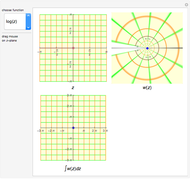
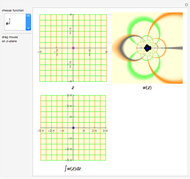
Snapshots
Details
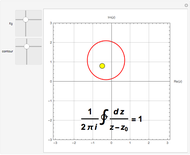
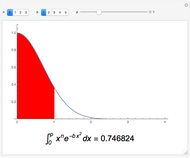
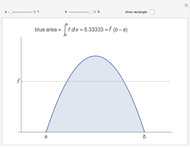
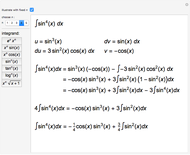
An integral of the complex plane is a line integral over a specified path  .
.
When the path of a complex line integral is a closed curve, the value of the integral can be evaluated using Cauchy's residue theorem,  , equal to
, equal to  times the sum of the residues inside the contour.
times the sum of the residues inside the contour.
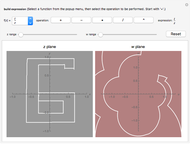
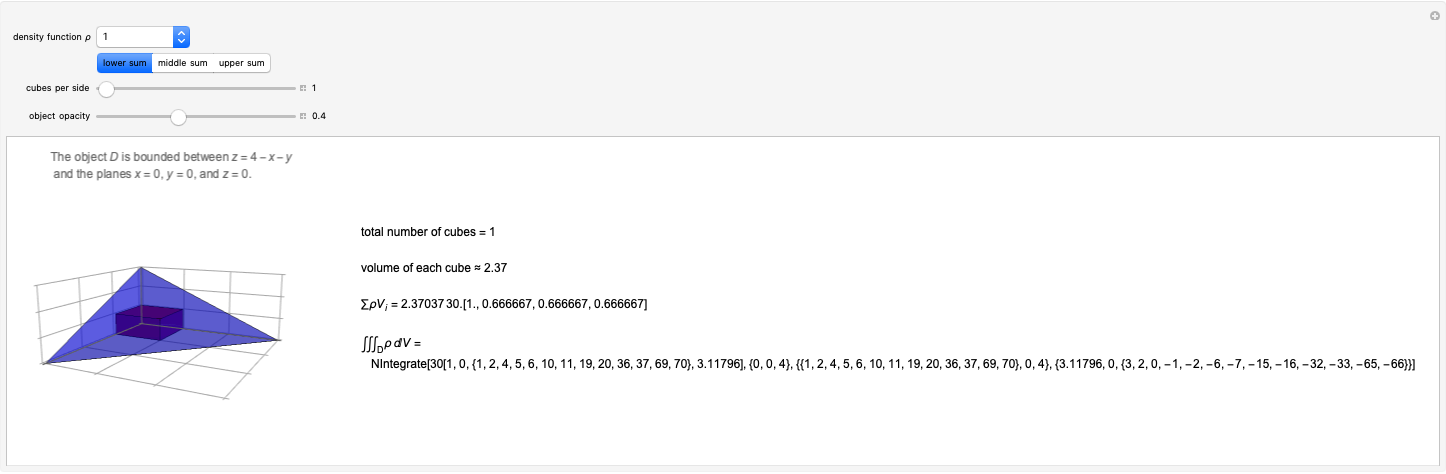
In this Demonstration, you can see that when the path of integration is closed, its image on the projected plane is also closed. But when the contour contains singularities, the image of the contour is topologically different from the original closed curve.
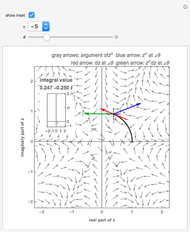
A singularity changes the number of rotations of the curve about the point; this is called the winding number. When the winding number is  , a clockwise loop is transformed to a counterclockwise loop. The contour integration is nonzero only in this case.
, a clockwise loop is transformed to a counterclockwise loop. The contour integration is nonzero only in this case.
Singularities, branch points and branch cuts are shown in pink in the  -plane; the singularity with winding number
-plane; the singularity with winding number  is shown as a magenta point.
is shown as a magenta point.
Reference
[1] T. Needham, Visual Complex Analysis, Oxford: Clarendon Press, 1998.
Permanent Citation