Contour Integral around a Simple Pole

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
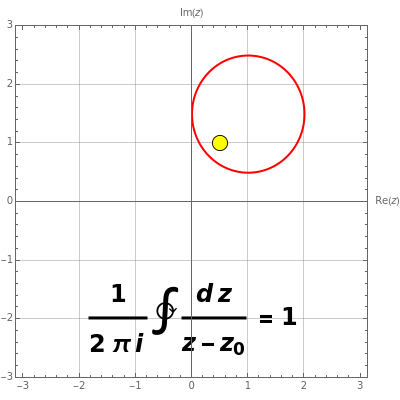
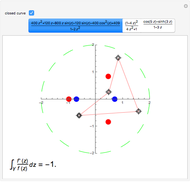
The function  is analytic in the entire
is analytic in the entire  plane, except for a simple pole at
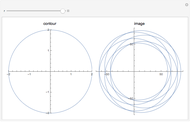
plane, except for a simple pole at  . The function is to be integrated counterclockwise over a unit circle, shown in red, which you can move in the complex plane. If the singular point
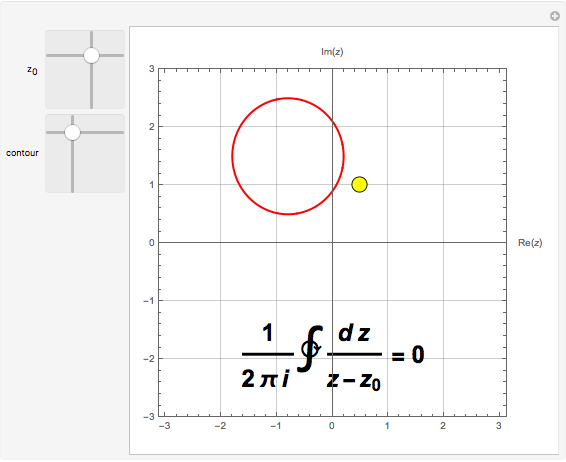
. The function is to be integrated counterclockwise over a unit circle, shown in red, which you can move in the complex plane. If the singular point 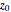 falls outside the contour of integration, the function is analytic everywhere on and inside the contour and the integral equals zero by Cauchy's theorem:
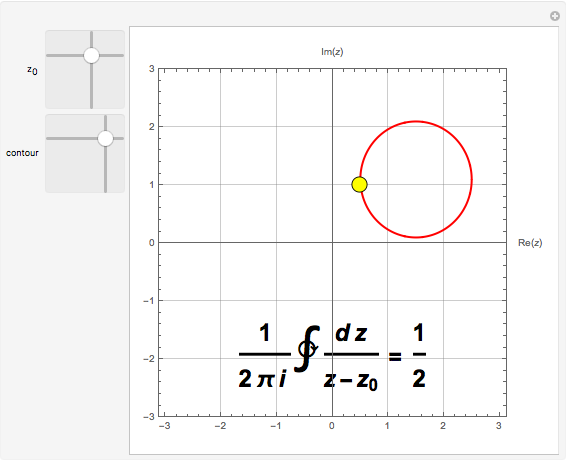
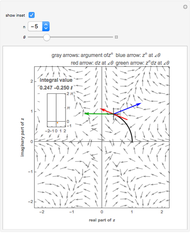
falls outside the contour of integration, the function is analytic everywhere on and inside the contour and the integral equals zero by Cauchy's theorem: 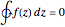 . When the singularity lies within the contour, the residue theorem applies and the integral equals 1. In the intermediate case, when the simple pole lies on the contour, it can be considered to be half inside, half outside. The Cauchy principal value for this segment of the integral is implied, so that the complete integral equals
. When the singularity lies within the contour, the residue theorem applies and the integral equals 1. In the intermediate case, when the simple pole lies on the contour, it can be considered to be half inside, half outside. The Cauchy principal value for this segment of the integral is implied, so that the complete integral equals  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
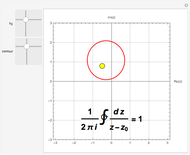
Snapshot 1: Cauchy integral formula with residue 1
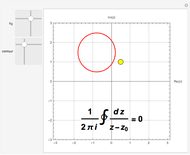
Snapshot 2: Cauchy's theorem gives 0
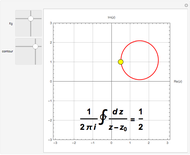
Snapshot 3: singularity lies on contour; integral equals 
Permanent Citation