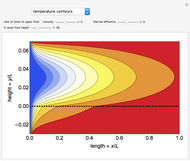
Mass Transfer between Adjacent Fluids in Laminar Flow

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
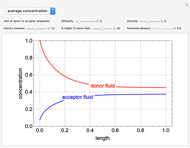
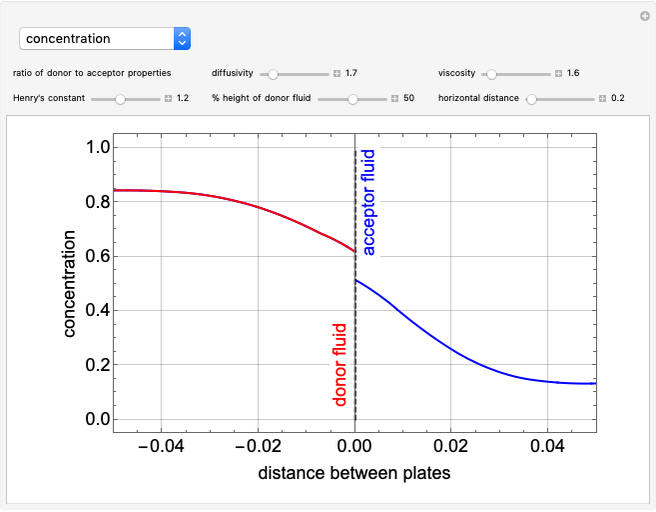
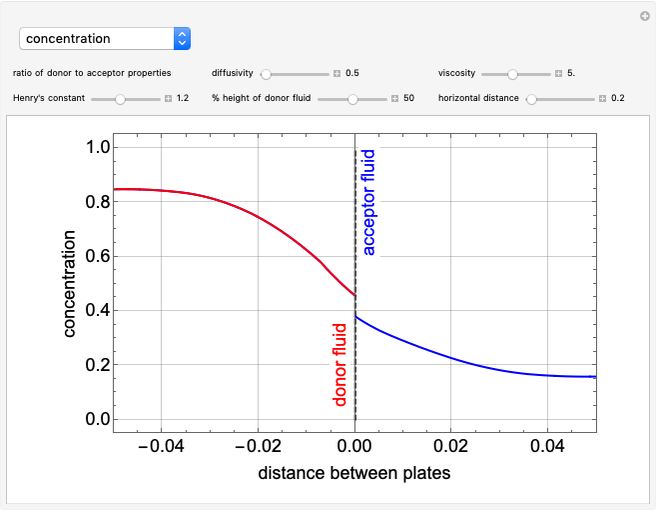
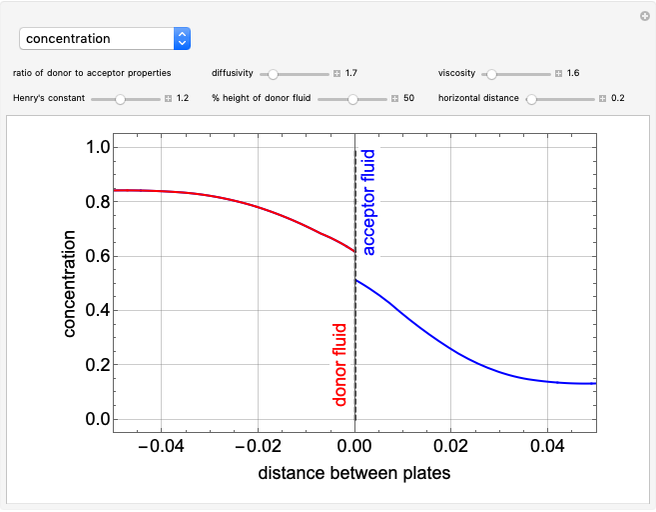
This Demonstration considers the vertical mass transfer of a substance between two adjacent immiscible solvents flowing horizontally in laminar flow between two parallel plates. The velocity and the concentration in both phases are shown as functions of the fluid properties, Henry's constant and the fraction of donor to acceptor fluids.
Contributed by: Clay Gruesbeck (June 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Assume that the properties of the two fluids are unchanged and that their velocity profiles are independent of horizontal location.
In the inlet region  , the liquids are in fully developed laminar flow and have different uniform concentrations
, the liquids are in fully developed laminar flow and have different uniform concentrations  and
and  ; in the region
; in the region  , the parallel plates do not permit mass transfer.
, the parallel plates do not permit mass transfer.
The concentration profile is:
 ,
where
,
where  is the velocity,
is the velocity,  is the concentration,
is the concentration,  is the diffusivity,
is the diffusivity,  is the horizontal distance along the plates and
is the horizontal distance along the plates and  is the vertical distance between the plates.
is the vertical distance between the plates.
Let  be the distance between the plates and
be the distance between the plates and  be the fraction filled with the lower fluid, with the interface at
be the fraction filled with the lower fluid, with the interface at  . Then the lower plate is at
. Then the lower plate is at  , the upper plate is at
, the upper plate is at  and the initial and boundary conditions are:
and the initial and boundary conditions are:
 ,
,
 ,
,

and
 .
Here
.
Here

and
 ,
where 1 and 2 represent the lower (donor) and upper (acceptor) fluid, respectively.
,
where 1 and 2 represent the lower (donor) and upper (acceptor) fluid, respectively.
Analytic solution for fully developed flow of two immiscible fluids between two flat plates when the fluids have arbitrary viscosity ratios and arbitrary flow rate ratios is derived in [1]:
 ,
,
 .
.
Here  is the horizontal pressure gradient and
is the horizontal pressure gradient and  and
and  are the viscosities of the lower and upper fluids; the average (cup) concentrations of the two fluids are:
are the viscosities of the lower and upper fluids; the average (cup) concentrations of the two fluids are:
 ,
,
 .
.
The concentration of the transferred species at the interface is  , where
, where  is Henry's constant. When
is Henry's constant. When  , the concentration is continuous across the interface; when
, the concentration is continuous across the interface; when  , the concentration of the transferred species is higher in the donor than in the acceptor fluid; and when
, the concentration of the transferred species is higher in the donor than in the acceptor fluid; and when  , the opposite is true and the donor fluid becomes the acceptor. Here we use
, the opposite is true and the donor fluid becomes the acceptor. Here we use  .
.
These equations are solved with the built-in Wolfram Mathematica function NDSolve, and plots of the concentration and velocity contours are shown.
Reference
[1] B. A. Finlayson. "Poiseuille Flow of Two Immiscible Fluids between Flat Plates with Applications to Microfluidics." (May 14, 2020) www.chemecomp.com/poiseuille_immiscible.pdf.
Permanent Citation