Median Split
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
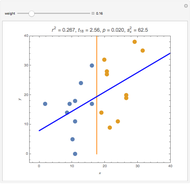
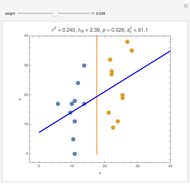
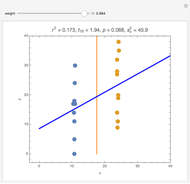
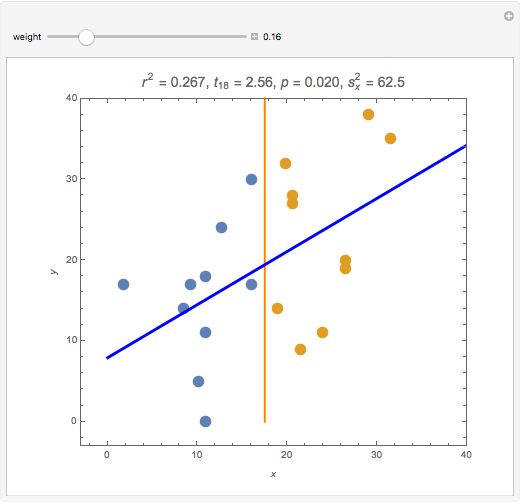
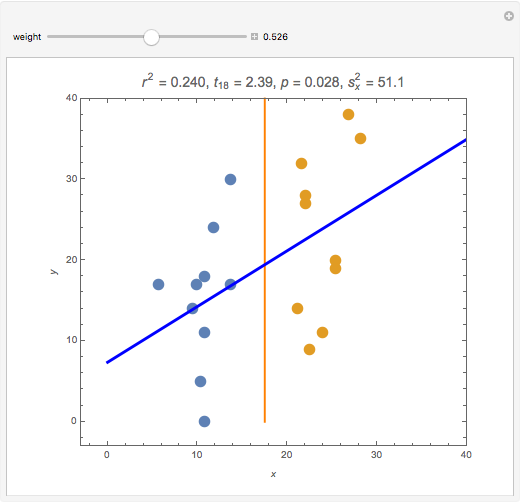
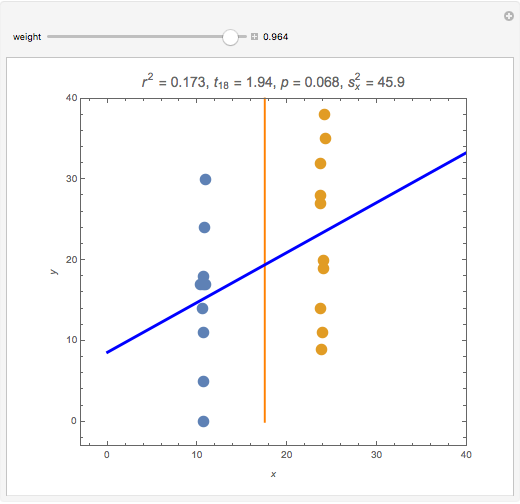
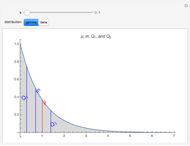
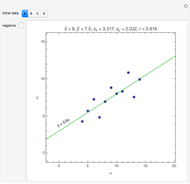
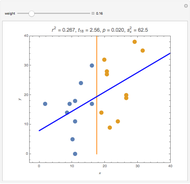
Splitting a continuous variable into two groups at its median is sometimes used in data analysis. On average, splitting a predictor variable 
is equivalent in correlation and regression to replacing all the 
values with either the mean 
value for the low group or the high group, as appropriate. Each data value 
is replaced by the weighted average 
, where 
is the mean for the group containing 
and 
is a weight value with 
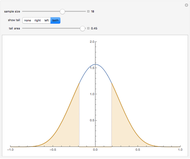
. Moving the weight slider to the right moves the 
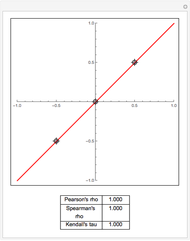
values toward a median split. Observe the decrease in 
, the 
-statistic, its 
-value, and the predictor's variance as the data is moved towards the equivalent of a median split. Much is lost and nothing gained by a median split.
Contributed by: Gary McClelland (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
It is interesting to observe the movement of points near each other and near the median. Moving the slider from left to right exaggerates the difference between those observations. At the same time, extreme observations are grouped together with observations near the median as the slider moves from left to right. Exaggerating the difference between observations that were originally close together while at the same time minimizing the differences between observations that were originally very far apart cannot possibly be a useful strategy for data analysis.
For further consideration of this example and other negative consequences of dichotomizing continuous variables, see:
J. R. Irwin and G. H. McClelland, "Negative Consequences of Dichotomizing Continuous Predictor Variables," Journal of Market Research, 40(3), 2003 pp. 366–371.
R. C. MacCallum, S. Zhang, K. J. Preacher and D. D. Rucker, "On the Practice of Dichotomization of Quantitative Variables," Psychological Methods, 7(1), 2002 pp. 19–40.
Permanent Citation
"Median Split"
http://demonstrations.wolfram.com/MedianSplit/
Wolfram Demonstrations Project
Published: March 7 2011
Visualizing the Exact Median Rank
Frederick Wu
Different Perspectives on the Median of a Distribution
Alexander White and Lawrence M. Lesser
Mean, Median, and Quartiles in Skewed Distributions
Ian McLeod
The Sampling Distribution of a Sampling Quantile
Seth J. Chandler
The r-Distribution
Chris Boucher
Exploring Measures of Association
Jeff Hamrick
Joint Density of Trivariate Gaussian Random Variables
John M. Shea
Joint Density of Bivariate Gaussian Random Variables
John M. Shea
Anscombe Quartet
Ian McLeod (University of Western Ontario)
Null Distribution of the Correlation Coefficient
Ian McLeod
