Methods of Social Choice

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
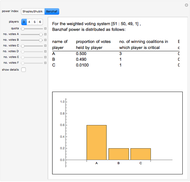
This Demonstration illustrates the outcomes of various social choice procedures. These procedures are used to reach a decision when there are more than two alternatives and none of those alternatives is the first choice of a majority of the voters. Quite often, for the given preference lists of the voters, the different procedures choose different winners. In addition to plurality, the standard methods of the Borda count, sequential pairwise voting with a fixed agenda (abbreviated SPFVA in the Demonstration), and the Hare method are illustrated. The option to have a dictator is included, as is information on whether a given set of voter preferences has a Condorcet winner.
Contributed by: Marc Brodie (March 2011)
(Benedictine University at Mesa)
Open content licensed under CC BY-NC-SA
Snapshots
Details
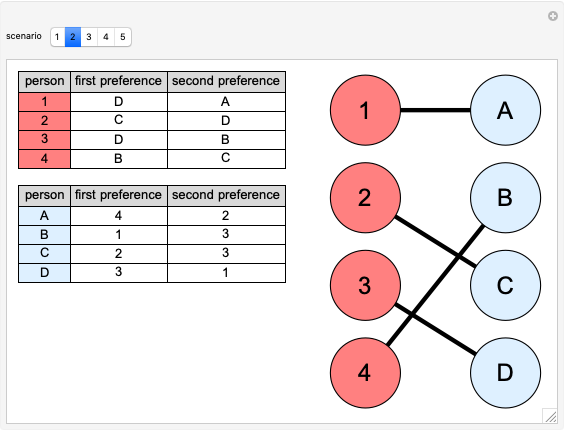
Given  alternatives, each voter ranks those alternatives into a strict "preference list".
alternatives, each voter ranks those alternatives into a strict "preference list".
To avoid ties in as many situations as possible, preference list 5 always has either 1 voter or two voters so as to make the total number of voters odd.
Some brief definitions:
The Borda count assigns points to each alternative, giving that alternative  points each time it is the first choice of a voter,
points each time it is the first choice of a voter,  points each time it is the second choice, etc. The alternative(s) with the most points is (are) declared the social choice.
points each time it is the second choice, etc. The alternative(s) with the most points is (are) declared the social choice.
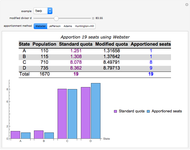
Sequential pairwise voting with a fixed agenda starts with a particular ordering of the alternatives (the fixed agenda). The first two alternatives on that list are compared in a "head-to-head" competition, and the alternative preferred by the majority of the voters survives to be compared with the third alternative. This procedure iterates until only one alternative remains and is declared the social choice. For given preference lists, different fixed agendas can result in different winners (see snapshots 2 and 3).
The Hare method iteratively deletes those alternatives that occur at the top of the fewest preference lists until one alternative is at the top of a majority of lists and is declared the winner.
A Condorcet winner is an alternative that would defeat each of the other alternatives in a head-to-head competition.
Reference
A. D. Taylor, Mathematics and Politics: Strategy, Voting, Power and Proof, New York: Springer 1995, for further details.
Permanent Citation