Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Minimal Enclosing Circle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

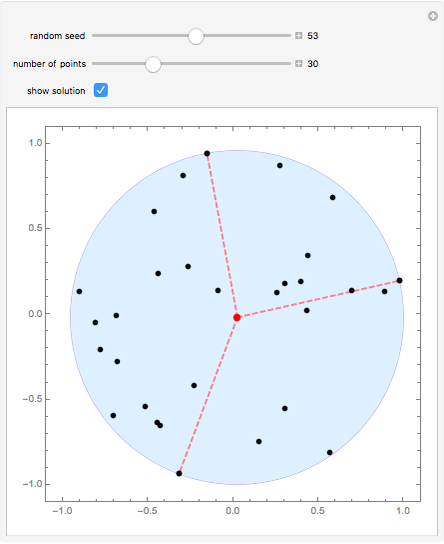
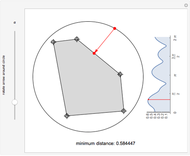
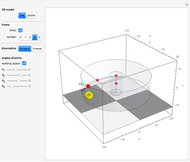
The minimal enclosing circle is the smallest circle that completely contains a set of points. Formally, given a set 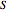of points in the plane, find the circle of smallest radius such that all points in 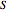are contained in the interior or boundary of .

Contributed by: Frederick Wu (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

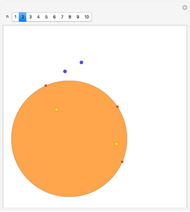
Snapshot 1: state the problem with a set of random points in the plane

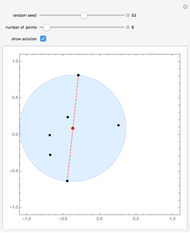
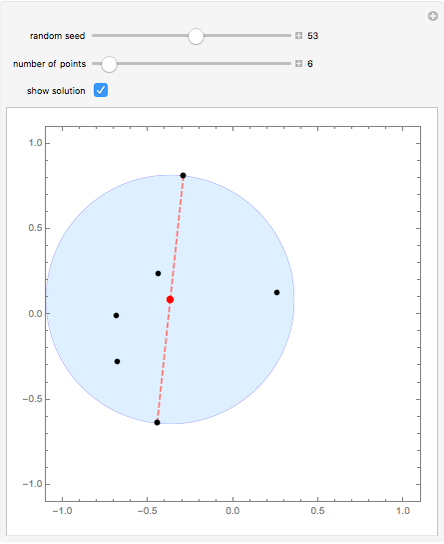
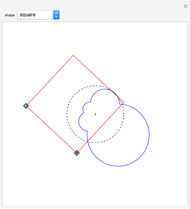
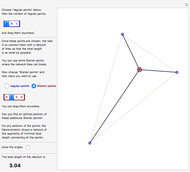
Snapshot 2: find the minimal enclosing circle with two points on its boundary

Snapshot 3: find the minimal enclosing circle with three points on its boundary

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send