Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Minimum of a Function Using the Fibonacci Sequence

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

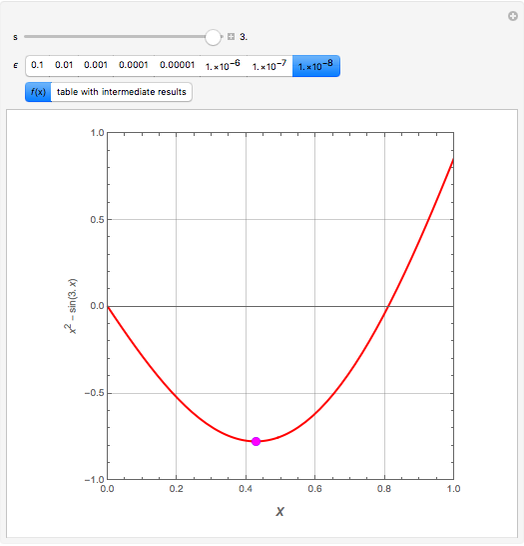
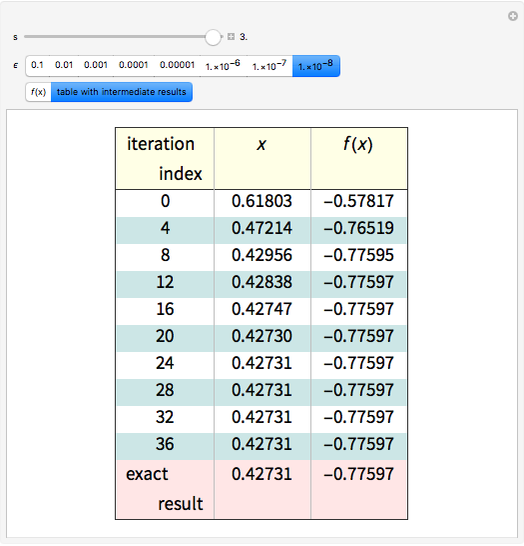
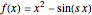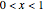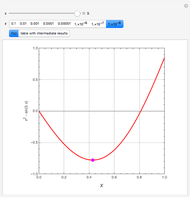
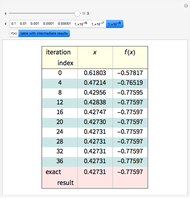
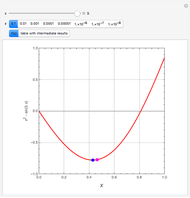
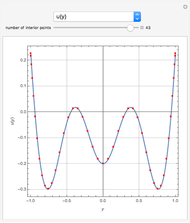
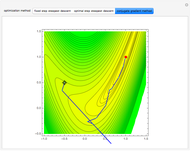
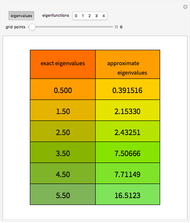
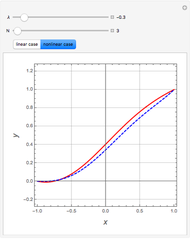
Consider the function , , where is a parameter. This Demonstration approximates the minimum of 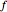using an algorithm based on the Fibonacci sequence, shown by a magenta point on the plot of 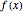. For comparison, the blue point is the minimum found by Mathematica's built-in function NMinimize. When is sufficiently small, there is good agreement.

[more]

You can vary the values of and (see the Details section for the definition of ). The Demonstration plots and you can see a table of points in the iteration of the algorithm.

[less]

Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (May 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Steps involved in a Fibonacci search:

1. Calculate 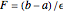, where 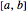is the interval in which 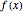is defined.

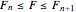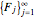2. Identify such that where is the Fibonacci sequence.

3. Set 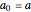and .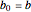

4. Calculate 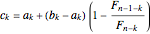and .

5. If , set and 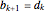; otherwise set and .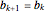

6. Set 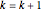and go to step 3.

7. Stop when .

Reference

[1] J. H. Mathews. "Module for the Fibonacci Search." (Apr 30, 2013) mathfaculty.fullerton.edu/mathews/n2003/FibonacciSearchMod.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send