Solution of a PDE Using the Differential Transformation Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider the partial differential equation (PDE)  with initial condition and boundary conditions
with initial condition and boundary conditions  and
and  ,
,  , and
, and  , where
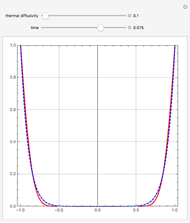
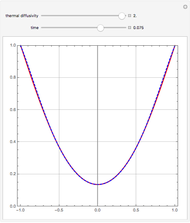
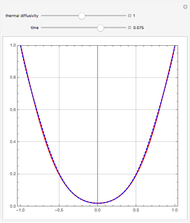
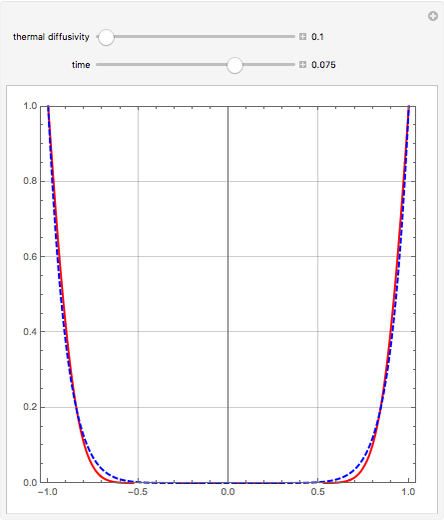
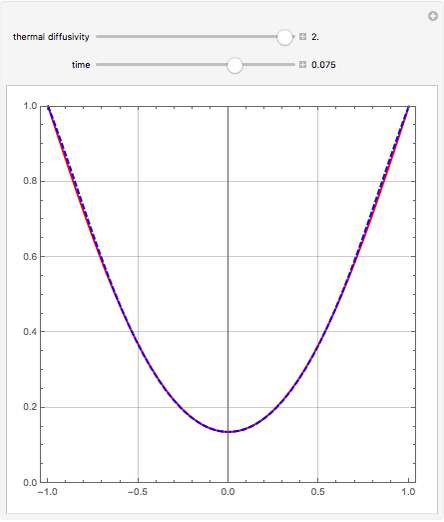
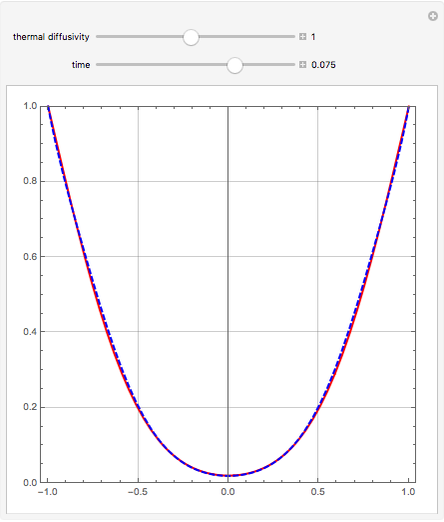
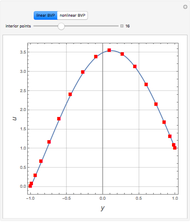
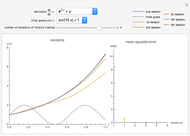
, where  is the thermal diffusivity. This problem represents the transient heat conduction in a slab. This Demonstration obtains the temperature profile
is the thermal diffusivity. This problem represents the transient heat conduction in a slab. This Demonstration obtains the temperature profile  for user-set values of the dimensionless time
for user-set values of the dimensionless time  and the thermal diffusivity
and the thermal diffusivity  . The red curve and the dashed blue curve are obtained using Mathematica's built-in function NDSolve and the differential transformation method (DTM), respectively. Here, the DTM gives reasonably good results despite its simplicity.
. The red curve and the dashed blue curve are obtained using Mathematica's built-in function NDSolve and the differential transformation method (DTM), respectively. Here, the DTM gives reasonably good results despite its simplicity.
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The  -order Taylor series expansion of
-order Taylor series expansion of  is of the form
is of the form  . If one takes
. If one takes  , the Maclaurin series of
, the Maclaurin series of  is
is  . The differential transformation
. The differential transformation  of the function
of the function  is given by
is given by  . The differential inverse transform of
. The differential inverse transform of  is defined by
is defined by  . Table 1 in [1] gives a list of properties of the differential transformation. In this Demonstration,
. Table 1 in [1] gives a list of properties of the differential transformation. In this Demonstration,  and
and  .
.
Reference
[1] C. L. Chen and Y. C. Liu, "Solution of Two-Boundary-Value Problems Using the Differential Transformation Method," Journal of Optimization Theory and Applications, 99(1), 1998 pp. 23–35. doi: 10.1023/A:1021791909142.
Permanent Citation