Minimum Surface Area of a Capped Hexagonal Prism

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
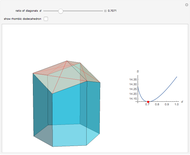
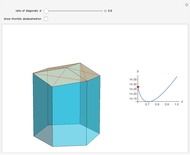
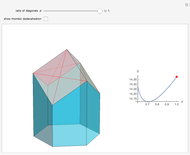
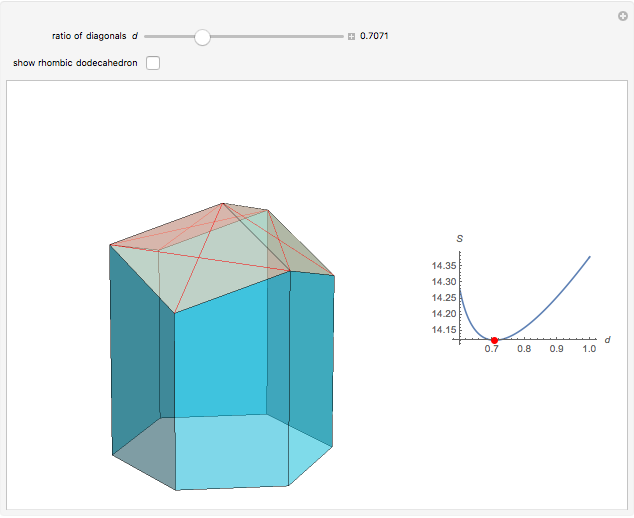
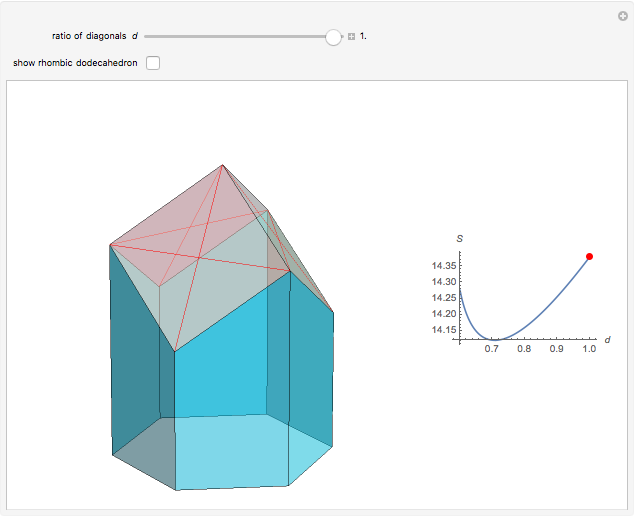
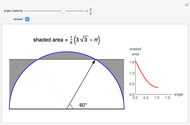
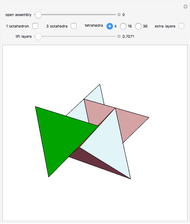
A hexagonal prism  is capped with three rhombi at one of its ends. The surface area of
is capped with three rhombi at one of its ends. The surface area of  , designated
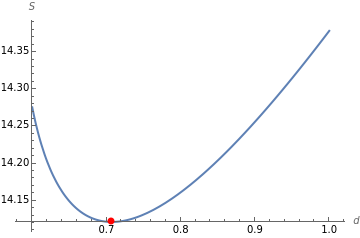
, designated  , is minimized when
, is minimized when  , the ratio of the diagonals of the rhombi, equals
, the ratio of the diagonals of the rhombi, equals  , which also pertains to the faces of the rhombic dodecahedron. Honeycombs are likewise characterized by this geometry.
, which also pertains to the faces of the rhombic dodecahedron. Honeycombs are likewise characterized by this geometry.
Contributed by: Sándor Kabai (August 2016)
Additional contribution by János Tóth
Open content licensed under CC BY-NC-SA
Snapshots
Details
The points that are movable are the top vertex and three of the vertices of the top hexagon, in the opposite direction. Let  be the magnitude of this vertical motion,
be the magnitude of this vertical motion,  be the height of the prism and
be the height of the prism and  be the ratio of diagonals of the rhombus. Then the surface area
be the ratio of diagonals of the rhombus. Then the surface area  is determined by:
is determined by:
 ,
,
 ,
,
 .
.
The surface area  has a minimum value when its derivatives with respect to
has a minimum value when its derivatives with respect to  equals zero.
equals zero.
References
[1] Archimedes Lab. "Puzzle #117: The Geometry of the Bees." (Aug 16, 2016) www.archimedes-lab.org/monthly_puzzles_ 72.html.
[2] F. Tóth, "What the Bees Know and What They Do Not Know," Bulletin of the American Mathematical Society, 70, 1964 pp. 468–481. www.ams.org/journals/bull/1964-70-04/S0002-9904-1964-11155-1/S0002-9904-1964-11155-1.pdf.
Permanent Citation