Montmort's Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
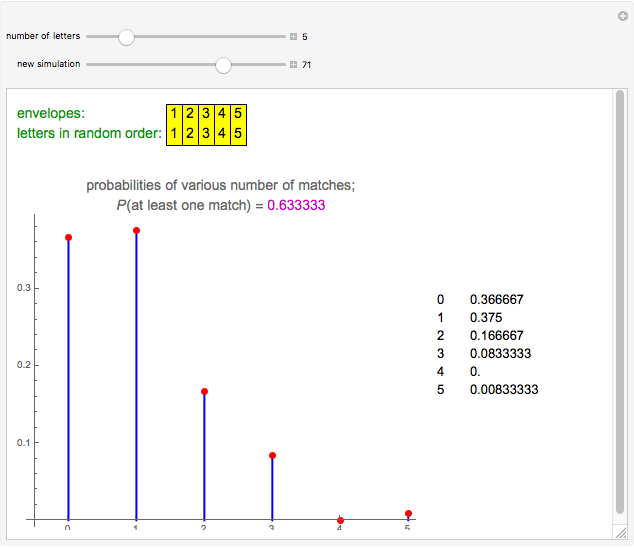
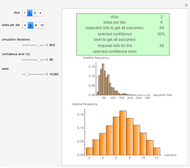
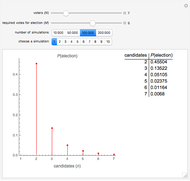
Mr. M. wrote a number of letters and prepared the corresponding envelopes. He then put the letters into the envelopes at random. How many letters will be in the correct envelope? The Demonstration shows the results of this experiment and the exact probabilities of the various numbers of correct matches.
Contributed by: Heikki Ruskeepää (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: With five letters, one experiment gave five matches, which has probability only about 0.8%. With  letters, exactly
letters, exactly  matches is impossible, because the
matches is impossible, because the  letter must also be in the correct envelope.
letter must also be in the correct envelope.
Snapshot 2: with 10 letters, there are some cases with four matches; here is one of them
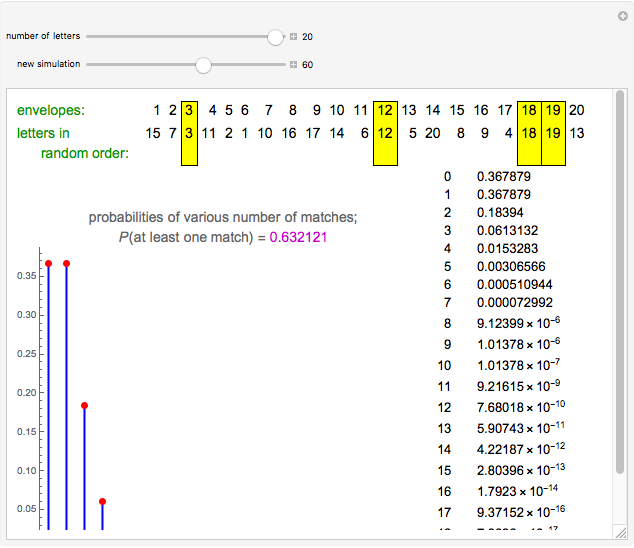
Snapshot 3: with 20 letters, there are also some cases with four matches; here is one of them
This problem has various names that contain words like Montmort, derangements, rencontres, matches, or coincidences; see, for example, [1, pp. 100–101], [2, pp. 68–73], [3, pp. 4–8, 231–236]. It was first considered and solved by Pierre Rémond de Montmort in 1708 and 1713. The problem is often represented, as here, by randomly putting letters into envelopes but also, say, by randomly giving hats to their owners.
The expected number of matches is always 1, irrespective of the number of letters. The variance is also always 1. The probability of at least one match approaches the value  . Already with five letters, the probability of at least one match is 0.6333, quite close to the limit. With five or more letters, the probability of at least five matches is very small. The distribution of the number of matches approaches the Poisson distribution with parameter 1.
. Already with five letters, the probability of at least one match is 0.6333, quite close to the limit. With five or more letters, the probability of at least five matches is very small. The distribution of the number of matches approaches the Poisson distribution with parameter 1.
References
[1] W. Feller, An Introduction to Probability Theory and Its Applications, Vol. I, 3rd ed., New York: Wiley, 1968.
[2] F. Mosteller, Fifty Challenging Problems in Probability with Solutions, New York: Dover, 1987.
[3] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton, NJ: Princeton University Press, 2008.
Permanent Citation