Nodal Surfaces of Degenerate States

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
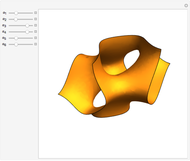
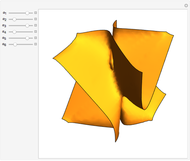
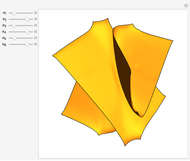
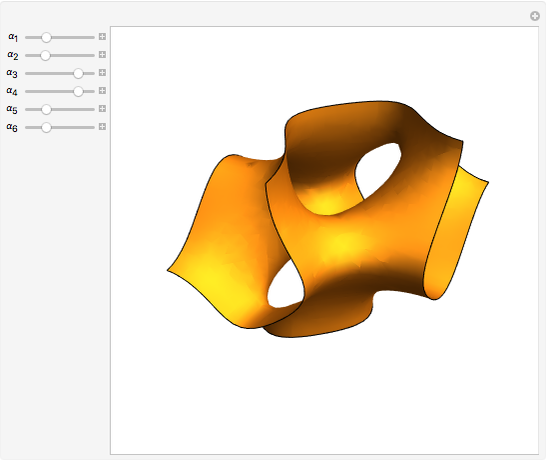
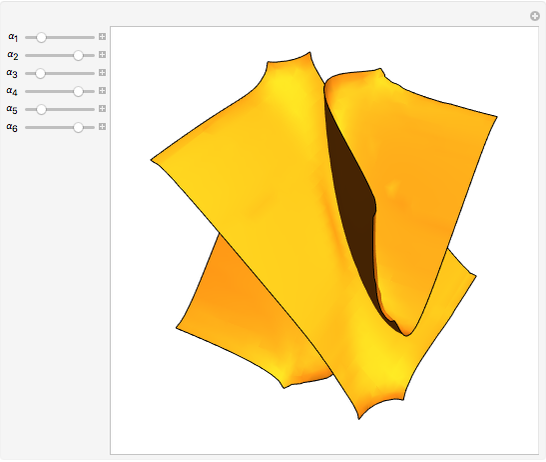
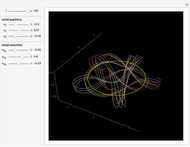
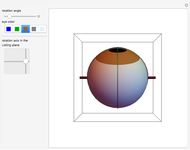
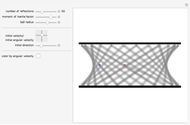
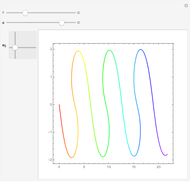
Nodal surface of a degenerate state in an 3D infinite square potential well. Degenerate solutions of an eigenvalue problem are linearly independent solutions to the same eigenvalue. For the Helmholtz equation within a cubical box with homogeneous Dirichlet boundary conditions, most states have sixfold degeneracy. This Demonstration allows the exploration of the space of possible nodal surfaces for a low‐lying state. The nodal surface is the eigenfunction zero locus.
Contributed by: Michael Trott (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
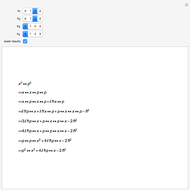
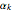 — coefficients in the superposition
— coefficients in the superposition 
Permanent Citation
"Nodal Surfaces of Degenerate States"
http://demonstrations.wolfram.com/NodalSurfacesOfDegenerateStates/
Wolfram Demonstrations Project
Published: March 7 2011