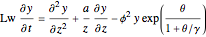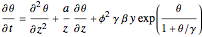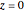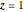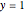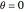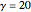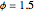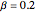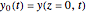Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Nonstationary Heat and Mass Transfer in a Porous Catalyst Particle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

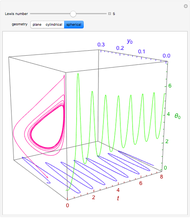
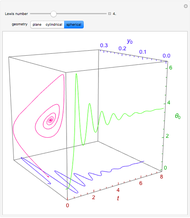
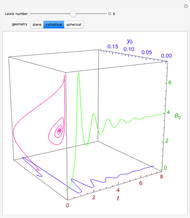
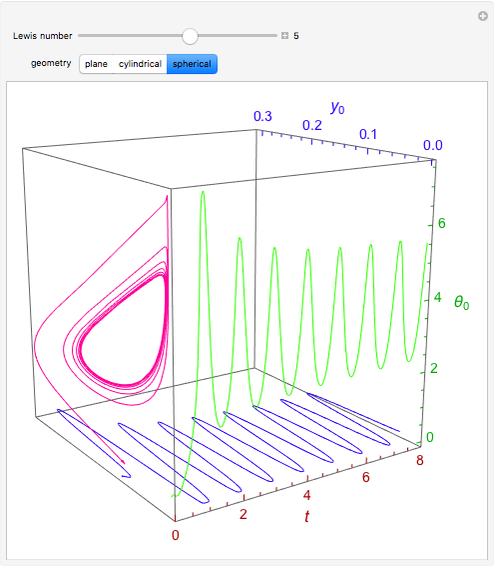
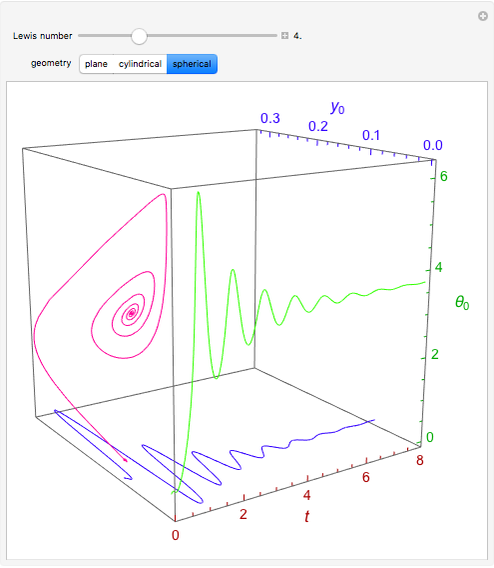
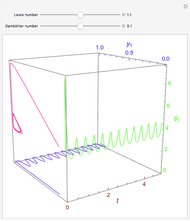
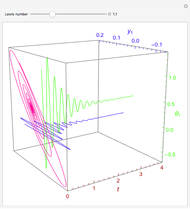
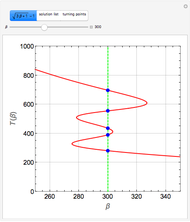
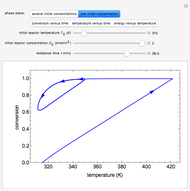
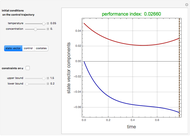
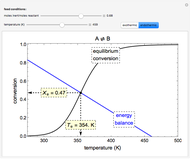
Consider the nonisothermal diffusion and reaction within a porous catalyst particle in which a first-order exothermic reaction takes place [1–4]. This system is governed by the following two dimensionless parabolic partial differential equations and boundary conditions BC1 and BC2:

[more]

,

,

BC1: : ,

BC2: : , .

Here is concentration and is temperature, is the activation energy, is the Thiele modulus, is the parameter of heat evolution, and is the Lewis number. The Thiele modulus relates catalytic activity to particle size. The Lewis number is the ratio of thermal to mass diffusivity. It is used to characterize fluid flows where there is simultaneous heat and mass transfer by convection. The parameter is 0, 1, or 2 for plane, cylindrical, or spherical symmetry, respectively. As can be seen from snapshot 1, periodic solutions are obtained for and . In the figure, and are plotted versus in blue and green, respectively. Also, you can see from snapshot 1 that a limit cycle is obtained for the above values of and .

[less]

Contributed by: Housam Binous, Abdullah A. Shaikh, and Ahmed Bellagi (February 2016)
(King Fahd University of Petroleum and Minerals, KSA; ENIM, University of Monastir, Tunisia)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] V. Hlaváček, M. Kubíček, and M. Marek, "Analysis of Nonstationary Heat and Mass Transfer in a Porous Catalyst Particle I," Journal of Catalysis, 15(1), 1969 pp. 17–30. doi:10.1016/0021-9517(69)90004-9.

[2] V. Hlaváček, M. Kubíček, and M. Marek, "Analysis of Nonstationary Heat and Mass Transfer in a Porous Catalyst Particle II," J. Catalysis, 15(1), 1969 pp. 31–42. doi:10.1016/0021-9517(69)90005-0.

[3] R. Aris, The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts, Vols. I and II. Oxford: Clarendon Press, 1975.

[4] M. Kubíček, and M. Marek, Computational Methods in Bifurcation Theory and Dissipative Structures, Springer Series in Computational Physics, New York: Springer-Verlag, 1983.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send