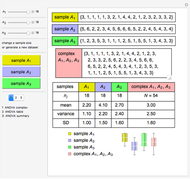
Numerical Example of One-Way ANOVA

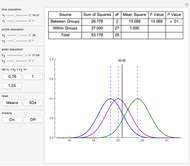
In ANOVA logic, partitioning the sources of variance and hypothesis testing can be done individually. According to the ANOVA method, the total variation is decomposed into two parts: a source of variation due to the group or factor effect (expressed with 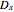) and a source of variation due to the measurement error (expressed with ).

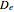This Demonstration uses the ANOVA table algorithm based on deviations.

By definition, the variance 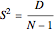, where 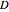is the sum of squared deviations; 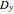is the total deviation, based on the differences between variants 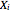and the mean of statistical complex; 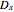is the intergroup or between-group deviation, based on differences between each group (or sample) and the complex means; and 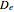is the intragroup or within-group deviation, based on differences between the variants 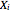and the sample (group) mean.

This Demonstration illustrates some basic principles of one-way ANOVA only. We know that the Fisher 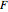-test is used for comparisons of the components of the total deviation. The 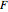-value is the ratio of variance between and variance within samples (groups).

Consider an experiment to study the effect of three different levels of a factor on a response 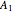, , 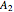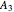. With 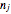(here we use but say there are groups) observations for each level, we write the outcome of the experiment in a work table.

To calculate the 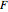-ratio:

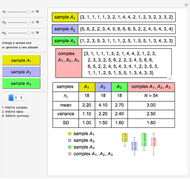
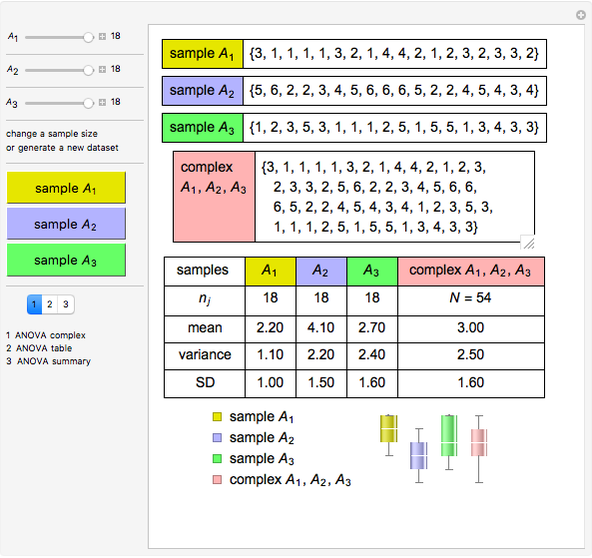
Calculate the size of the statistical complex (first row in the work table) .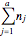

Calculate the sum within each sample (group), and the complex total sum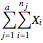, adding values in the row.

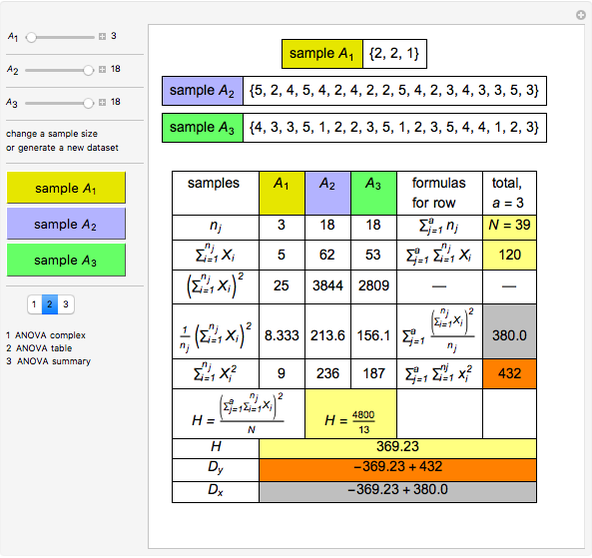
Calculate 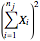, the square of the sum.

Find the value 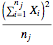and the total sum in the row:

.

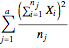Calculate the 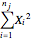(sum of square).

Find the total sum in the row .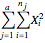

Find the value :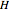

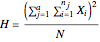
and the deviations:

,

,

.

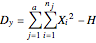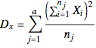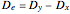Calculate total variance 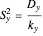, between-group variance 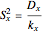, and within-group variance .

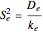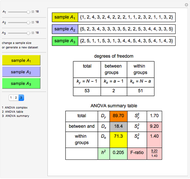
The statistical ANOVA complex degrees of freedom is .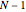

The between-group degrees of freedom is one less than the number of groups (samples): .

The within-group degrees of freedom is .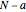

And finally we find the 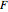-ratio:

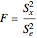
and the relative factor effect:

.

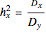It is well known that the 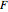-test is used to compare the components of the total deviation. In this Demonstration, we are using the textbook method of concluding the hypothesis test: compare the observed 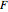-value with the critical value of 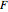determined from tables. The critical value of 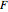is a function of the numerator degrees of freedom, the denominator degrees of freedom, and the significance level alpha. If the experimental 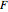-value is more than critical 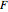-value, then reject the null hypothesis.

The Demonstration has thus illustrated how we can get and apply the experimental 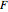-value.

References

[1] A. Gelman, "Analysis of Variance—Why It Is More Important Than Ever," Annals of Statistics, 33(1), 2005. pp. 1–53. doi:10.1214/009053604000001048.

[2] D. C. Montgomery, Design and Analysis of Experiments, 5th ed., New York: Wiley, 2001.