Olbers's Paradox

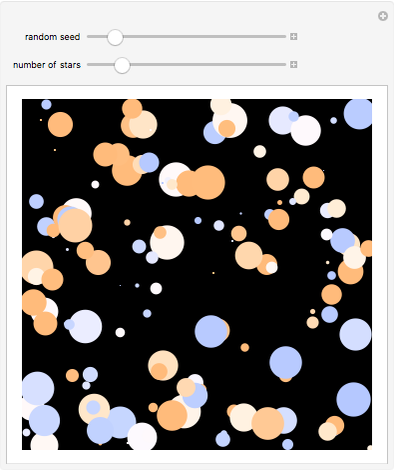
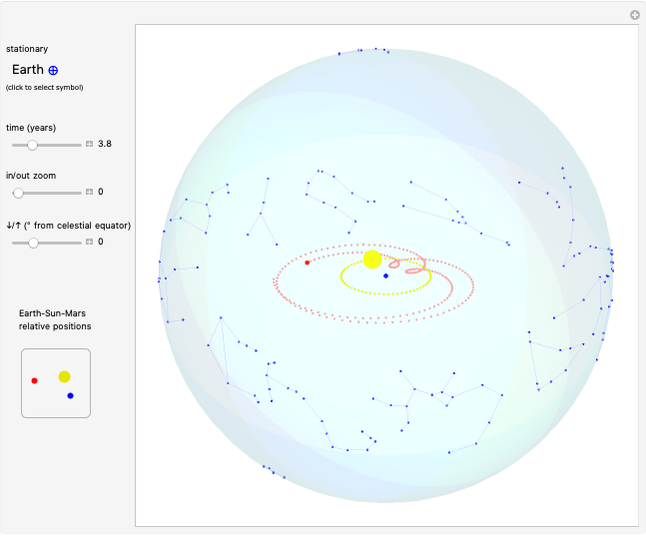
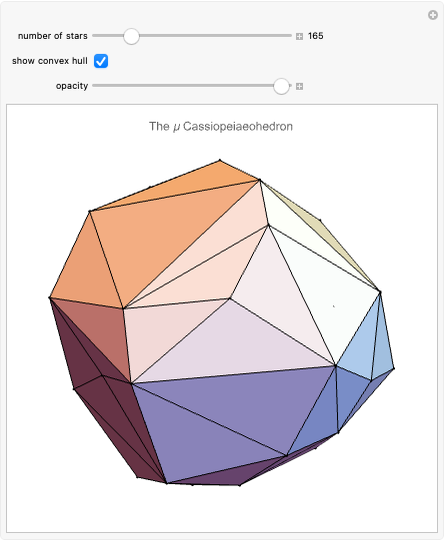
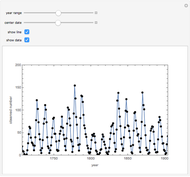
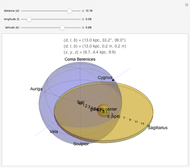
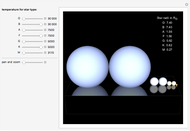
If the universe were eternal and infinite in all directions, then every line of sight from the Earth should eventually intersect a star and the entire sky should be as bright as the Sun. This has become known as Olbers's paradox (ca. 1826), although it had been addressed earlier by Kepler and Halley. Referring to what we actually see, this can also be called the "dark-night-sky paradox."

There is, as yet, no simple canonical resolution of the paradox, but one or more factors might be involved. Most fundamentally, astronomers and cosmologists now believe that the universe began with the Big Bang and is therefore finite in both space and time. But it might still be possible for an immensely large, though finite, number of stars to light up the sky. Some cosmologists suggest that the most distant stars might be receding faster than the speed of light, so that they are beyond the visible horizon. This might also be tied in with the universe's accelerating rate of expansion. Another contributing factor might be the red shift of light from the most distant stars, which might show up as a contribution to the cosmic microwave background (CMB).