Plant Pathogen and Hyperparasite Annual Cycle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
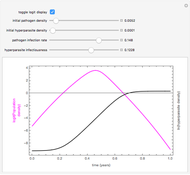
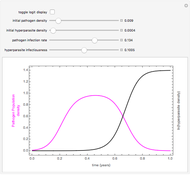
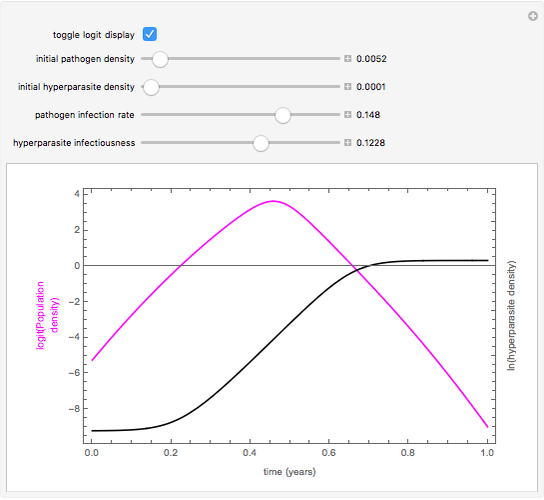
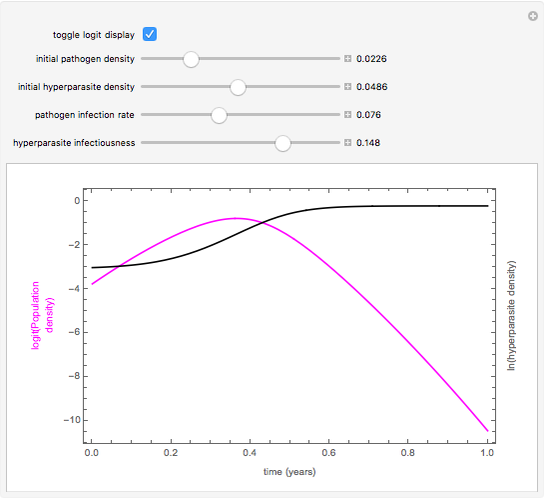
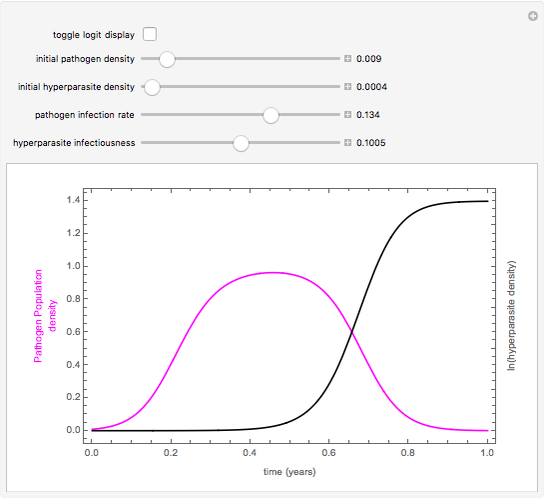
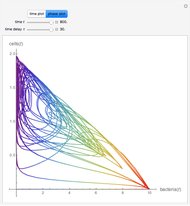
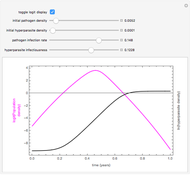
This Demonstration shows the annual cycle of a population of a plant pathogen that is itself attacked by a hyperparasite. The pathogen increases at a per capita rate that is reduced in proportion to the population size and decreases during the season as conditions become progressively unfavorable. It is destroyed by a hyperparasite at a rate that is proportional to both populations. The growing season is assumed to be 180 days. The hyperparasite harms the pathogen and multiplies by destroying it, but has no in-season death rate. This models something with long-lived structures but only one food source.
Contributed by: Michael Shaw (March 2011)
Open content licensed under CC BY-NC-SA
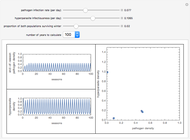
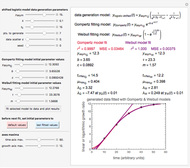
Snapshots
Details
If the pathogen population as a proportion of its maximum is  and the population of the hyperparasite is
and the population of the hyperparasite is  , and both are functions of time
, and both are functions of time  , the equations governing the changes in time are:
, the equations governing the changes in time are:
 ,
,
 , and
, and
 ,
,  .
.
Permanent Citation