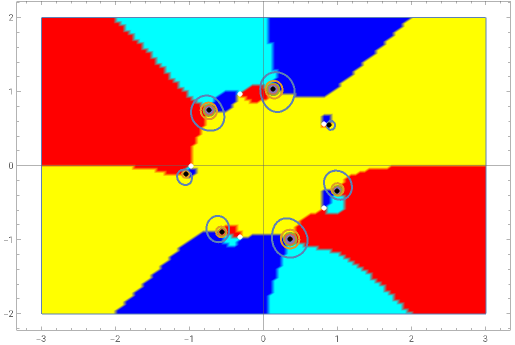
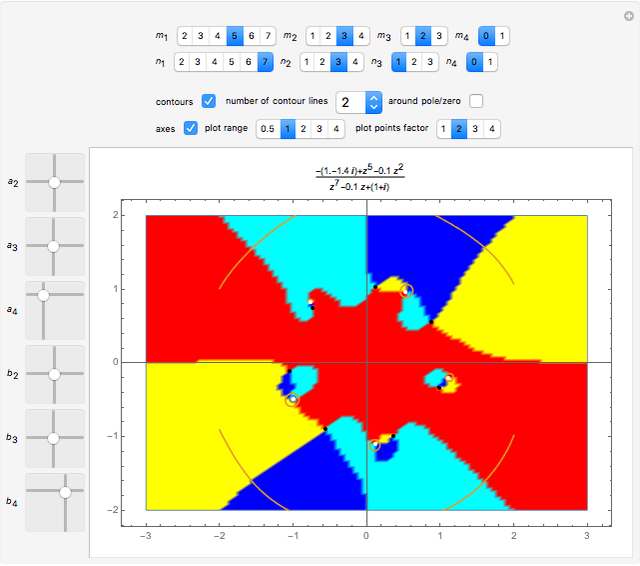
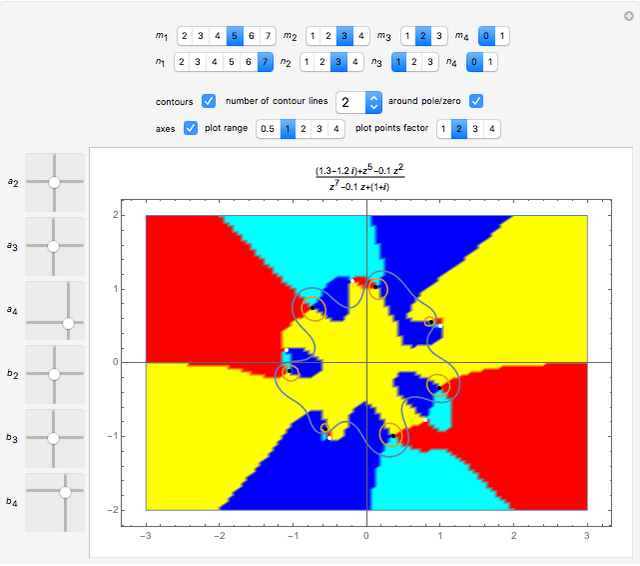
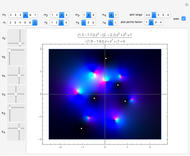
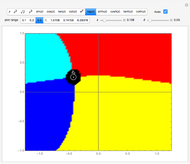
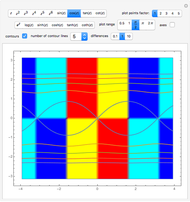
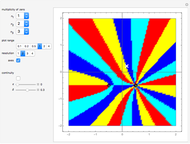
This Demonstration shows a complex rational function as a contour plot superposed on a parametric plot, in which colors depend on the quadrant in which falls. A rational function is the quotient of two polynomials, and . This Demonstration uses polynomials of the form and , where the coefficients and are complex numbers. Suppose that and have no common roots. Then the zeros of are the zeros of , and the zeros of are the poles of . Zeros are shown in white in the centers of the black patches, and poles are shown as black points.