Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Portfolio Diversification Benefit from Subadditive VaR

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

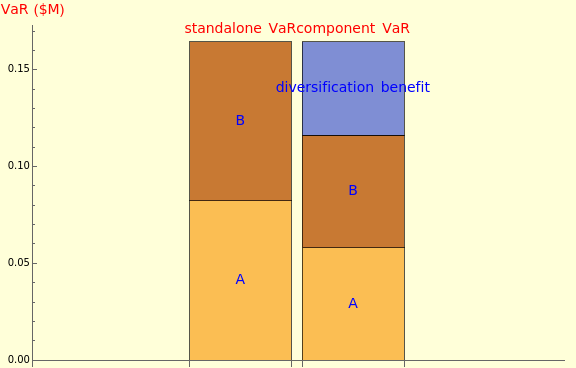
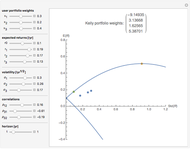
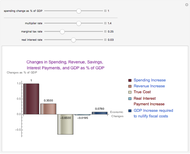
Portfolio diversification benefit derives from investing in various assets whose values do not rise and fall in perfect harmony. Because of this imperfect correlation, the risk of a diversified portfolio is smaller than the weighted average risk of its constituent assets. In term of Value at Risk (VaR), portfolio VaR is smaller than the sum of its constituent VaRs because VaR is a subadditive risk measure: .

[more]

Consider a simple portfolio worth $1 million, invested in two assets ( and ), with relative weights . The assets have volatilities and are correlated by such that their variance-covariance matrix is .

Assuming zero asset returns (a reasonable assumption given a short-term investment horizon), the standalone VaR can be calculated: , where is the standard normal variate at 100% () confidence level, assuming the asset returns are normally distributed (e.g. at 95% confidence level VaR).

The portfolio VaR is calculated as .

Portfolio VaR can be attributed to component assets as component VaRs, which enjoy the additive property and sum to portfolio VaR: . In general, component VaR of the asset is defined as .

[less]

Contributed by: Pichet Thiansathaporn (July 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

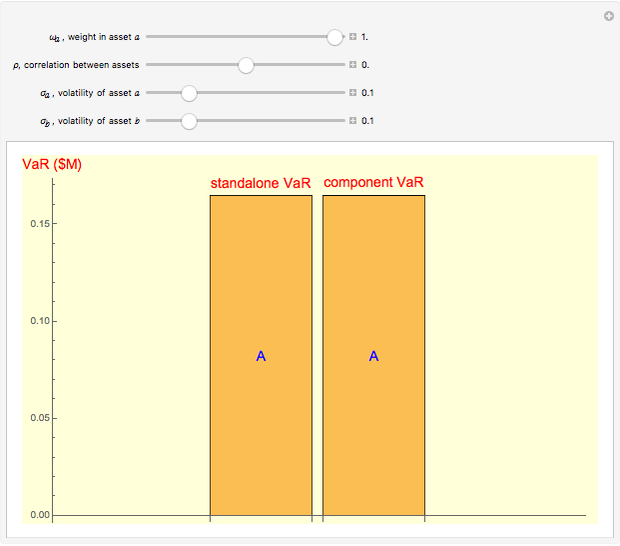
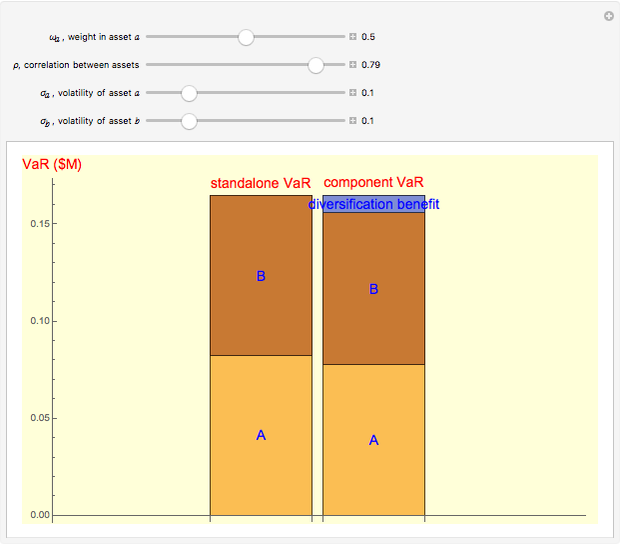
Snapshot 1: when assets are perfectly correlated (), there is no diversification benefit and

Snapshot 2: when assets are less than perfectly correlated (), there is some diversification benefit and

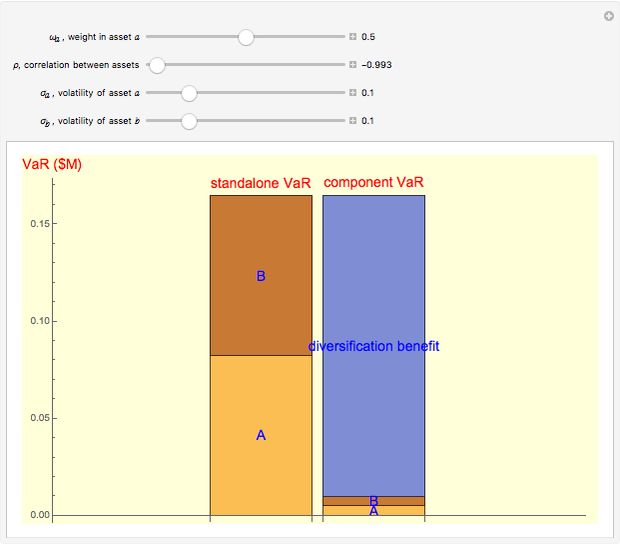
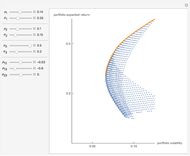
Snapshot 3: when assets are perfectly contrarian (), the diversification benefit is maximized

Snapshot 4: when assets are over concentrated ( or ), the diversification benefit is reduced

Snapshot 5: assets that are negatively correlated with other assets in the portfolio can serve as a natural hedge, since they contribute negatively to portfolio VaR (i.e. their component VaRs are negative)

Reference

[1] Kevin Dowd, Measuring Market Risk, 2nd ed., West Sussex, England: Wiley, 2005 pp. 271–274.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send