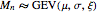Generalized Extreme Value Distributions: Application in Financial Risk Management

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
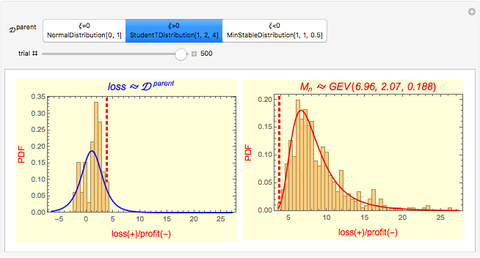
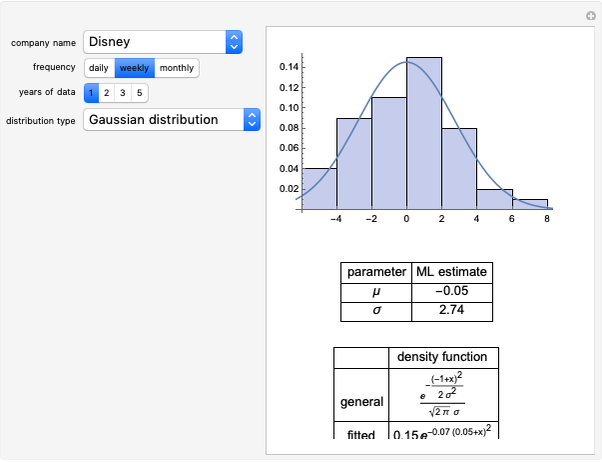
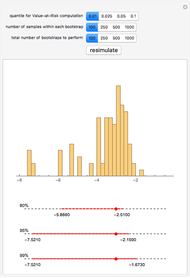
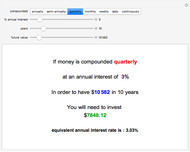
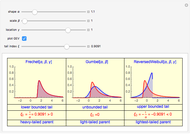
This Demonstration illustrates the Fisher–Tippett–Gnedenko theorem in the context of financial risk management. A sample of  observations is drawn from a parent distribution
observations is drawn from a parent distribution 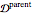 that describes the probability of historical losses of a portfolio (left-hand plot). A number of draws (
that describes the probability of historical losses of a portfolio (left-hand plot). A number of draws ( ) are repeated to obtain a histogram of 500 maximal losses (
) are repeated to obtain a histogram of 500 maximal losses ( ), shown as a running cumulative in the right-hand plot. At each draw, the position of
), shown as a running cumulative in the right-hand plot. At each draw, the position of  is marked by a red vertical dashed line.
is marked by a red vertical dashed line.
Contributed by: Pichet Thiansathaporn (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] K. Dowd, Measuring Market Risk, 2nd ed., West Sussex, England: Wiley, 2005 pp. 190–194.
Permanent Citation