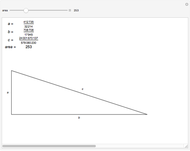
Positive Frobenius Numbers of Three Arguments

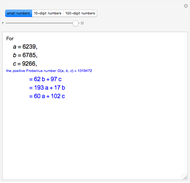
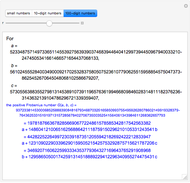
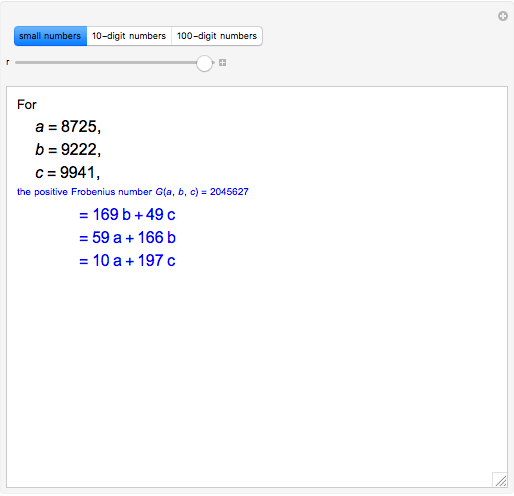
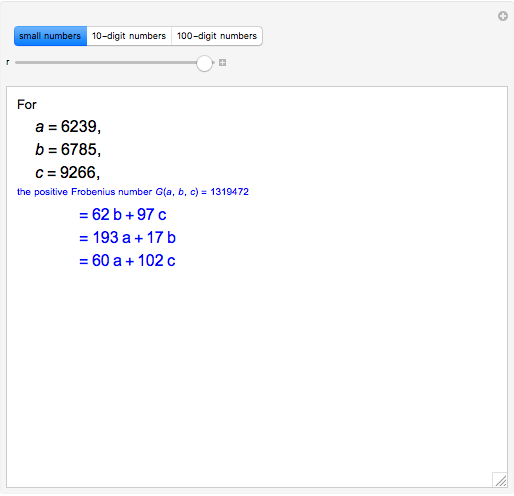
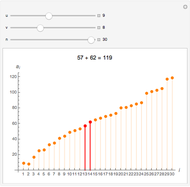
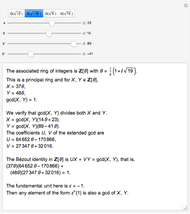
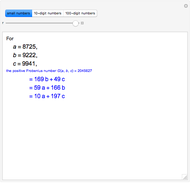
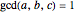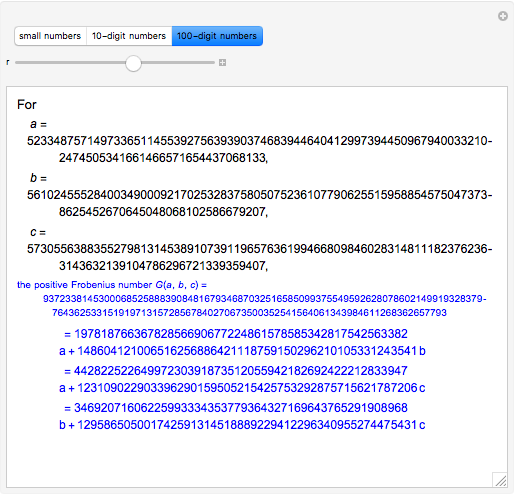
Let , , be three positive integers with . It is well-known that all sufficiently large integers are representable as positive linear combinations of , , . Consider 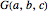, the positive Frobenius number of , , , defined to be the largest integer not representable as a positive linear combination of , , . Then 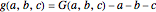is the usual Frobenius number, that is, the largest integer not representable as a non-negative linear combination , , . ( 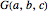differs from the positive Frobenius number 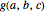in that multipliers for linear combinations of larger integers are allowed to be zero.) The function 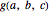corresponds to the Mathematica built-in function FrobeniusNumber[a,b,c].

We assume that , , are pairwise prime. This Demonstration computes and represents in three ways as positive linear combinations of (1) , , (2) , , and (3) , .