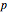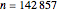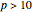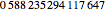Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Cyclic Numbers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

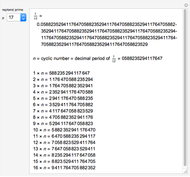
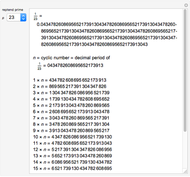
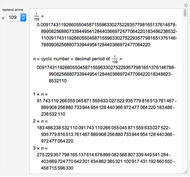
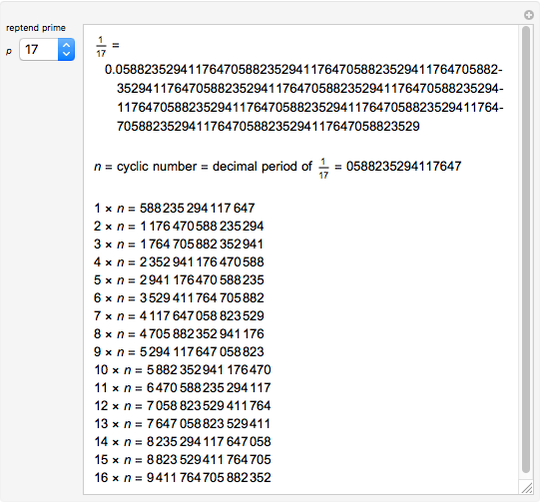
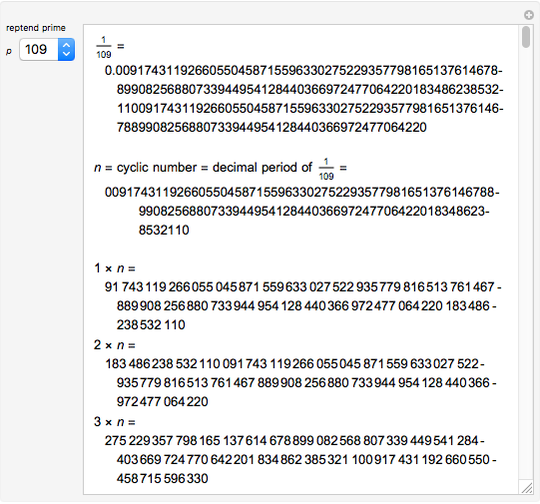
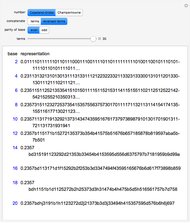
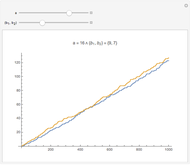
This Demonstration shows the first 10 cyclic numbers.

[more]

A cyclic number with digits is such that its digits are shifted cyclically when multiplied by an integer up to . For example, with , ; multiplying by 6 shifts the digits of by three places: . The decimal representation of the reciprocal of has a period of maximum length . So .

For , leading zeros are needed for . For example, the second cyclic number (which comes from ) is the integer .

[less]

Contributed by: Izidor Hafner (December 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

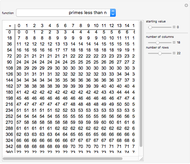
The first 10 values of that produce maximum period decimal expansions (with digits) for 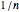are the reptend primes 7, 17, 19, 23, 29, 47, 59, 61, 97 and 109 [1, pp. 171–175].

References

[1] D. G. Wells, The Penguin Dictionary of Curious and Interesting Numbers, New York: Penguin Books, 1991.

[2] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. "Full Reptend Primes: Primes with Primitive Root 10." oeis.org/A001913.

[3] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. "Numbers with Digits Such That the First Multiples Are Cyclic Permutations of the Number, Leading 0's Omitted (or Cyclic Numbers)." oeis.org/A180340.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send