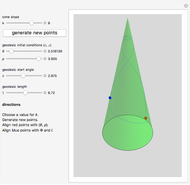
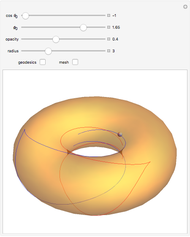
Pseudosphere Geodesics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
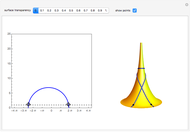
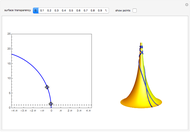
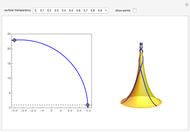
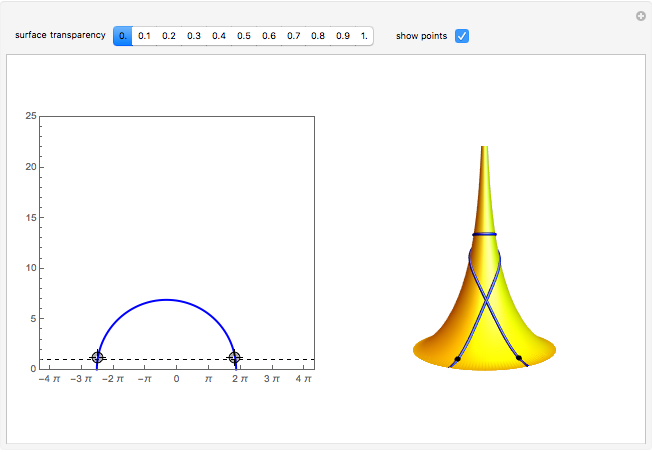
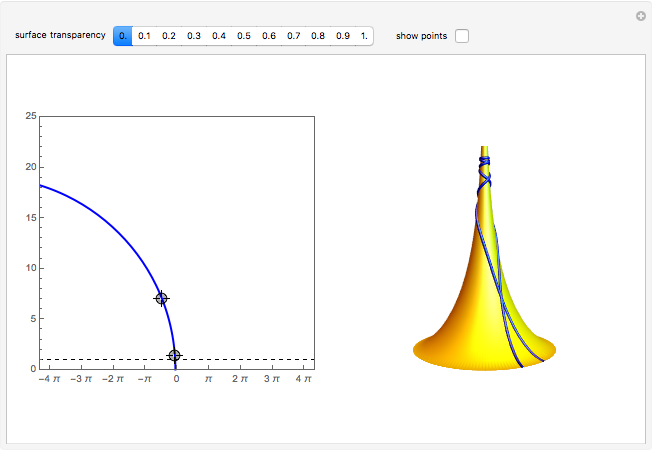
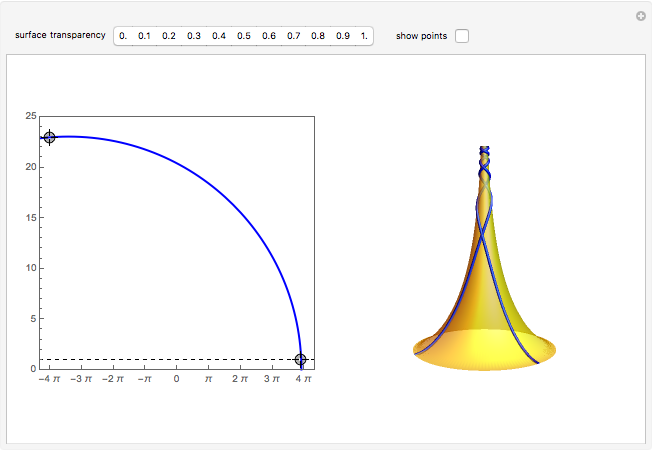
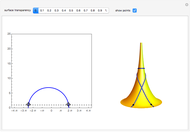
The pseudosphere is the surface obtained by revolving a tractrix around its asymptote. In a suitable parametrization, the first fundamental form of the pseudosphere is the same as in Poincaré's half-plane model of hyperbolic geometry. Each pair of points in Poincare's half-plane is joined by a unique geodesic that is either a vertical line or a circular arc with center on the horizontal axis. Geodesics on the pseudosphere are then easily obtained by mapping the lines and circular arcs onto the surface. The pseudosphere does not correspond to the whole upper half-plane but only to the region  . The fact that the pseudosphere can serve as a model for hyperbolic geometry was discovered by Eugenio Beltrami.
. The fact that the pseudosphere can serve as a model for hyperbolic geometry was discovered by Eugenio Beltrami.
Contributed by: Antonin Slavik (August 2013)
(Charles University, Prague)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A tractrix in the  -
- plane, whose asymptote is the
plane, whose asymptote is the  axis and which intersects the
axis and which intersects the  axis at a unit distance from the origin, can be parametrized as
axis at a unit distance from the origin, can be parametrized as  ,
,  , where
, where  . Rotating this curve around the
. Rotating this curve around the  axis, we end up with the pseudosphere, whose first fundamental form is
axis, we end up with the pseudosphere, whose first fundamental form is  ; this relation introduces a metric in the
; this relation introduces a metric in the  -
- half-plane, which coincides with the metric in Poincaré's half-plane model.
half-plane, which coincides with the metric in Poincaré's half-plane model.
The  coordinate of a point on the pseudosphere represents the angle of rotation around the asymptote of the tractrix. The parametrization has period
coordinate of a point on the pseudosphere represents the angle of rotation around the asymptote of the tractrix. The parametrization has period  in
in  and every point on the pseudosphere corresponds to infinitely many points in the
and every point on the pseudosphere corresponds to infinitely many points in the  -
- plane. Consequently, there are infinitely many geodesics joining a given pair of points on the pseudosphere.
plane. Consequently, there are infinitely many geodesics joining a given pair of points on the pseudosphere.
For more details, see Example 9.3.3 and Section 11.1 in [1]. The role of the pseudosphere in the history of hyperbolic geometry is described in [2].
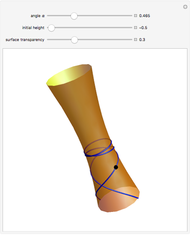
Making the surface semitransparent gives a better overview of the geodesic behavior, but takes longer to render.
References
[1] A. Pressley, Elementary Differential Geometry, 2nd ed., London: Springer, 2010.
[2] J. Stillwell, Mathematics and Its History, 3rd ed., London: Springer, 2010.
Permanent Citation